Heterodox
This post, as suggested, extends this one-good example. I assume a constant returns-to-scale technology, as specified in Tables 1 and 2. Labor is advanced to the capitalists, and wages are paid out of the surplus at the end of the year (period of production). The capitalists (incorrectly) expect the technology in existence at the start of the year to continue to exist. I assume prices of (re)production prevail. Table 1: Inputs for The Technology InputProcess(I)(II)(III)Labor30 eσ0,1(1 - t)180 eσ0,2(1 - t)(39/2) eσ0,3(1 - t)New Widgets100One-Year Old Widgets010Two-Year Old Widgets001 Table 2: Outputs for The Technology OutputProcess(I)(II)(III)New Widgets3 eσ1,1(t - 1)(7/4) eσ1,2(t - 1)(237/20) eσ1,3(t - 1)One-Year Old Widgets100Two-Year Old Widgets010 Only a newly produced widget is a
Topics:
Robert Vienneau considers the following as important: Austrian School Of Economics, Example in Mathematical Economics, Sraffa Effects, Towards Complex Dynamics
This could be interesting, too:
Robert Vienneau writes Another Hayekian Triangle Not Supporting The Austrian School
Robert Vienneau writes Roger Garrison On The Inadequacy Of Hayekian Triangles
Robert Vienneau writes The Production Of Commodities And The Structure Of Production: An Example
Robert Vienneau writes The Production Of Commodities And The Structure Of Production
|
This post, as suggested, extends this one-good example. I assume a constant returns-to-scale technology, as specified in Tables 1 and 2. Labor is advanced to the capitalists, and wages are paid out of the surplus at the end of the year (period of production). The capitalists (incorrectly) expect the technology in existence at the start of the year to continue to exist. I assume prices of (re)production prevail.
| Input | Process | ||
| (I) | (II) | (III) | |
| Labor | 30 eσ0,1(1 - t) | 180 eσ0,2(1 - t) | (39/2) eσ0,3(1 - t) |
| New Widgets | 1 | 0 | 0 |
| One-Year Old Widgets | 0 | 1 | 0 |
| Two-Year Old Widgets | 0 | 0 | 1 |
| Output | Process | ||
| (I) | (II) | (III) | |
| New Widgets | 3 eσ1,1(t - 1) | (7/4) eσ1,2(t - 1) | (237/20) eσ1,3(t - 1) |
| One-Year Old Widgets | 1 | 0 | 0 |
| Two-Year Old Widgets | 0 | 1 | 0 |
Only a newly produced widget is a consumer good. Old widgets can be used in production for two more years. The economic lifetime of a widget (machine) may be less than its physical life. Free disposal is assumed. I define techniques:
- Alpha: The widget is discarded after one year.
- Beta: The widget is discarded after two years.
- Gamma: The widget is discarded after three years.
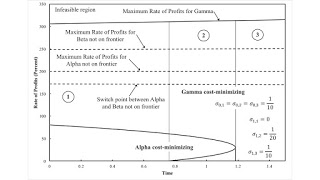
The specification of technology allows for productivity to increase in each process, both because labor is saved and because more output is produced with a unit input of widgets. Figure 1 shows one of my pattern diagrams, in which the specification of increased productivity results from reducing the parameter space to three dimensions.
I identify two of my patterns in this diagram, a pattern over the wage axis and a reswitching pattern. In Region 2, reswitching occurs. Around the switch point at the lower rate of profits, a higher rate of profits is associated with a truncation of the economic life of a machine to one years. This logical possibility contradicts Austrian capital theory, in which a scarcity of capital results in a higher rate of profits and a longer period of production. In circulating capital models, the switch point at the lowest rate of profits is 'non-perverse', unlike here. I thing Ian Steedman made the same observation decades ago.