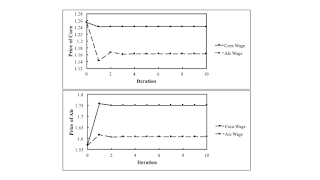
Figure 1: Prices of Corn and Ale in an Iterative Process1.0 Introduction Anwar Shaikh proposed, sometime in the 1970s, I guess, an interpretation of Marx's transformation problem. Marx's solution in volume 3 of Capital is the first step of an iterative process. I thought I might work through this idea with an example from an old exposition of mine. I am not sure how faithful I am to Shaikh's approach. I notice that as I explain it, the equality of total values and of total prices is maintained for gross output. In this conception, Marx's solution to the transformation problem is not incorrect or incoherent, but merely incomplete. My favorite solution to the transformation problem is based on von Charasoff's original capital, also known as Sraffa's standard commodity. Both Shaikh and
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics, Karl Marx
This could be interesting, too:
Robert Vienneau writes Austrian Capital Theory And Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes Double Fluke Cases For Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes The Emergence of Triple Switching and the Rarity of Reswitching Explained
Robert Vienneau writes Recap For A Triple -Switching Example
| Figure 1: Prices of Corn and Ale in an Iterative Process |
Anwar Shaikh proposed, sometime in the 1970s, I guess, an interpretation of Marx's transformation problem. Marx's solution in volume 3 of Capital is the first step of an iterative process. I thought I might work through this idea with an example from an old exposition of mine. I am not sure how faithful I am to Shaikh's approach. I notice that as I explain it, the equality of total values and of total prices is maintained for gross output. In this conception, Marx's solution to the transformation problem is not incorrect or incoherent, but merely incomplete.
My favorite solution to the transformation problem is based on von Charasoff's original capital, also known as Sraffa's standard commodity. Both Shaikh and Sraffa's solution raise a question about what is special about labor. As I understand it, Shaikh's iterative procedure does not need to start at labor values. One needs to look outside what is formalized in the mathematics.
2.0 Technology and Labor ValuesConsider a simple capitalist economy that produces only two goods, corn and ale. Assume the amounts of corn and ale produced each year are given, as well as the production processes used in each industry. Corn and ale are each produced by processes that require a year to complete. These processes require a certain number of workers to be hired at the beginning of the year, as well as the purchase of certain quantities of corn and ale to be used as inputs in production. Operating these processes then produces certain quantities of outputs of corn and ale for use at the end of the year. Table 1 shows the amount of inputs per unit output for both industries. The data allow for surplus production, that is for more corn and ale to be produced than are used as inputs. I might as well assume Constant Returns to Scale (CRS).
| Input | Corn Industry | Ale Industry |
| Labor | 1 Person-Year | 1 Person-Year |
| Corn | 1/8 Bushel | 3/8 Bushel |
| Ale | 1/16 Bottle | 1/16 Bottle |
| Output | 1 Bushel | 1 Bottle |
I now want to consider a couple of levels at which these processes can be operated. Suppose the first process is scale to produce a gross output of 15/16 bushels, and the second process is used to produce 1/16 bottles. Then the quantity flows shown in Table 2 result. With these gross outputs, one person-year is employed throughout the economy. The ale used up in production is exactly replaced by the output of ale industry. 9/64 bushels of the corn produced replace the corn used up in production. So these quantity flows are for a stationary state in which one person-year of labor are used to produce a net output of 51/64 bushels of corn. So a bushel of corn embodies 64/51 ≈ 1.255 person-years per bushel. If the wage consists entirely of corn, the maximum wage is 51/64 bushels per person-years.
| Input | Corn Industry | Ale Industry |
| Labor | 15/16 Person-Year | 1/16 Person-Year |
| Corn | 15/128 Bushel | 3/128 Bushel |
| Ale | 15/256 Bottle | 1/256 Bottle |
| Output | 15/16 Bushel | 1/16 Bottle |
On the other hand, suppose that 3/10 bushels of corn are produced in the corn industry, and 7/10 bottles are produced in the ale industry. The quantity flows shown in Table 3 result. Here, too, one person-year is employed throughout the economy. The corn produced is wholly used to replace the corn used as inputs throughout the economy. The net output of the ale industry, after replacing the ale used as capital goods, is 51/80 bottles. That is, a bottle of ale embodies 80/51 ≈ 1.569 person-years per bottle. The maximum wage is 51/80 bottles per person-years.
| Input | Corn Industry | Ale Industry |
| Labor | 3/10 Person-Year | 7/10 Person-Year |
| Corn | 3/80 Bushel | 21/80 Bushel |
| Ale | 3/160 Bottle | 7/160 Bottle |
| Output | 3/10 Bushel | 7/10 Bottle |
Labor values are 64/51 ≈ 1.255 person-years per bushel and 80/51 ≈ 1.569 person-years per bottle.
3.0 An Iterative ProcedureTo specify the iterations of prices, a general notation is useful. Accordingly, define the following variables.
- a0: A two-element row vector of direct labor coefficients.
- A: A 2x2 Leontief matrix.
- q: A two-element column vector of gross outputs.
- y: A two-element column vector of net outputs.
- w: A two-element column vector of the commodity wage.
- p: A two-element row vector of prices. Indexed in the iterative process.
- Cn: Constant capital, evaluated at prices in the iterative process.
- Vn: Variable capital, evaluated at prices in the iterative process.
- Sn: Surplus product, evaluated at prices in the iterative process.
The rate of profits is defined in terms of the ratio of surplus value to the value of the capital advanced. Both the numerator and the denominator are aggregated across all industries. Accordingly, I find it convenient to specify the level and composition of the economy as such that employment is one person-year, and the net output of the economy is in the proportions of the wage basket. These assumptions are more restrictive, I think, than is needed. Anyways, for this exposition of the first case, suppose quantity flows are as in Table 2. And let the commodity wage be at a level where half the net output is paid out as the wage. In this case, only corn is a consumption good.
Initially, prices are assumed to be labor values. The price of constant capital, at a given iteration, is:
Cn = pnA q
The value of advanced wage goods, at a given iteration, is:
Vn = pnw a0q
The value of surplus value is the value of net output not paid out to the workers:
Sn + Vn = pny
I take wages as advanced, along with constant capital. Accordingly, the overall rate of profits at a given iteration, is:
rn = Sn/(Cn + Vn)
Prices are iterated as follows:
pn + 1 = pn (A + w a0)(1 + rn)
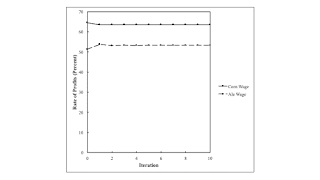
Notice that all the terms on the right-hand side are defined at a given iteration. Table 4 shows the results for the first few iterations in the case of the numeric example, with the assumptions for the first case.
| Count | p1 (approx.) | p2 (approx.) | S/(C + V) (approx.) |
| 0 | 64/51 | 80/51 | 0.645570 |
| 1 | 1.242244 | 1.758501 | 0.634923 |
| 2 | 1.242776 | 1.750519 | 0.635368 |
| ... | ... | ... | ... |
| 1.242755 | 1.750839 | 0.635350 |
As I understand, this iteration occurs in logical time. It is not a process in historical time. This process converges to prices of production, which satisfy the following equation:
p (A + w a0)(1 + r) = p
Marx sets out the first iteration above. One can modify the assumptions. I do not think much is gained by restricting attention to schemes of simple and expanded production, as at the end of Volume 2 of Capital.
| Figure 2: Rate of Profits in an Iterative Process |
In Figures 1 and 2, the lines labeled 'Corn Wage' are for the quantity flows in Table 2. The lines labeled 'Ale Wage' are for the quantity flows in Table 3. I suppose a better numeric example would not converge as quickly.
4.0 ConclusionThis post is one more illustration that academics have had ways of making sense of the transformation problem. One could argue about which way is more insightful. Do these discussions help make sense of capitalist economies and of the confusions in mainstream economics?
References- Deepankar Basu. 2020. Can commodities be substance of value? UMass Economics Working Papers. 290.
- Fred Moseley. 2020. A critique of Shaikh's two interpretations of Marx's 'transformation problem'. Cambridge Journal of Economics.
- Anwar Shaikh. 1977. Marx's theory of value and the 'transformation problem'. The Subtle Anatomy of Capitalism (ed. by Jesse Schwartz).
 Heterodox
Heterodox