Heterodox
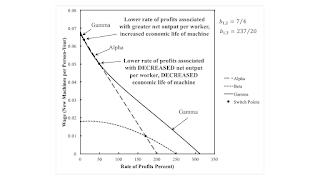
Figure 1: The Wage-Rate of Profits Frontier1.0 Introduction This is one in a series of posts demonstrating that the change in the economic life of a machine at a switch point is independent of the change of the capital intensity of the technique at a switch point. I want to illustrate each entry in a two-by-two table in a previous post. The example in this post has two switch points. One fits the traditional Austrian and neoclassical stories, as in the entry in the upper-left of the table. The other switch point is 'perverse' in both ways, as in the entry in the lower right. 2.0 Technology The example is of a 'one-good' economy, in which the produced commodity has a physical lifetime of three years when used in production. When the commodity is newly produced, it can also be used by
Topics:
Robert Vienneau considers the following as important: Austrian School Of Economics, Example in Mathematical Economics, Sraffa Effects
This could be interesting, too:
Robert Vienneau writes Another Hayekian Triangle Not Supporting The Austrian School
Robert Vienneau writes Roger Garrison On The Inadequacy Of Hayekian Triangles
Robert Vienneau writes The Production Of Commodities And The Structure Of Production: An Example
Robert Vienneau writes The Production Of Commodities And The Structure Of Production
 |
| Figure 1: The Wage-Rate of Profits Frontier |
This is one in a series of posts demonstrating that the change in the economic life of a machine at a switch point is independent of the change of the capital intensity of the technique at a switch point. I want to illustrate each entry in a two-by-two table in a previous post. The example in this post has two switch points. One fits the traditional Austrian and neoclassical stories, as in the entry in the upper-left of the table. The other switch point is 'perverse' in both ways, as in the entry in the lower right.
2.0 TechnologyThe example is of a 'one-good' economy, in which the produced commodity has a physical lifetime of three years when used in production. When the commodity is newly produced, it can also be used by households as a consumption good. I make the usual assumption of constant returns to scale. Each column of Table 1 shows the inputs for a production process operated at unit level. The corresponding columns show the outputs for each production process, again operated at a unit level. The efficiency of this machine varies over its lifetime.
| Input | Process | ||
| (I) | (II) | (III) | |
| Labor | 30 | 180 | 39/2 |
| New Widgets | 1 | 0 | 0 |
| One-Year Old Widgets | 0 | 1 | 0 |
| Two-Year Old Widgets | 0 | 0 | 1 |
| Output | Process | ||
| (I) | (II) | (III) | |
| New Widgets | 3 | b1, 2 | b1, 3 |
| One-Year Old Widgets | 1 | 0 | 0 |
| Two-Year Old Widgets | 0 | 1 | 0 |
The economic life of a machine may be less than its physical life. I assume free disposal. Three techniques can be defined:
- Alpha: The machine is discarded after one year.
- Beta: The machine is discarded after two years.
- Gamma: The machine is discarded after three years.
A system of equations defines prices of production for each technique. For example, the following two equations characterize the Beta technique:
(1 + r) + 30 w = 3 + p2
p2 (1 + r) + 180 w = b1, 2
Wages are assumed to be paid out of the product. A common rate of profits is charged on the prices of the capital goods advanced. The revenues recorded on the right-hand side are as appropriate for joint production. The price of a two-year old machines do not appear in the equations. Under Beta, two-year old machines are discarded, and their price is zero.
Given an externally specified rate of profits, the system of equations for each system can be solved for the wage and the prices of the old machines that are used in the production processes for that technique. Figure 1, at the top of this post, graphs the wage curves for the three techniques, for the values of b1, 2 and b1, 2 examined in this post. The cost-minimizing technique at any rate of profits is the technique that contributes its wage curve to the outer frontier. At a (non-fluke) switch point, two techniques are cost-minimizing. This example is a reswitching example.
 |
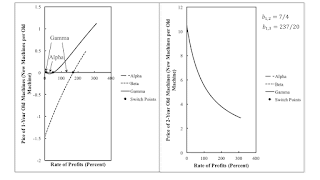
| Figure 2: The Prices of Old Machines |
The prices of old machines provide an equivalent method of analyzing the choice of technique with fixed capital. For each technique, the price of a new machine is unity. Figure 2 graphs the price of old machines. The left panel shows the price of a one-year old machine for the Beta and Gamma techniques, the two techniques in which such machines are operated. The right panel shows the price of a two-year old machine for the Gamma technique. The Gamma technique is only cost-minimizing in the range up to the maximum rate of profits when the price of old machines is positive or zero. That is Gamma is cost minimizing outside the two indicated switch points.
Consider the range for the rate of profits between the switch point. Gamma is not cost-minimizing here, and the economic life of a machine is truncated from its physical life. Beta is not cost-minizing in this range either, for the price of a one-year old machine is negative, under the system of equations for Beta prices. Consequently, the Alpha technique is cost-minimizing between the indicated switch points. (I thought a bit about how to draw a flowchart for a market algorithm for this example.) The analysis of the choice of technique with the construction of the outer wage frontier yields the same results as an analysis of truncation based on negative prices for old machines.
Two switch points exist on the outer envelope of the wage curves. For the first switch point, Alpha is preferred at a slightly higher rate of profits, and Gamma is preferred at a slightly lower rate of profits. That is, a lower rate of profits around the switch point results in the operation of the machine for a longer economic life of a machine. It also results in a cot-minimizing technique requires a greater value of capital per worker, and an increase in output per head.
All of this is reversed at the second switch point. A lower rate of profits around this switch point is associated with a shorter economic life of the machine, a smaller value of capital per worker, and a decrease in output per head.
4.0 ConclusionThis post has filled in two entries in a two-by-two table. In these entries, either output per head and the economic life of a machine rise with a higher wage around a switch point. Or, in contrast to traditional marginalist and Austrian theory, they both fall with a higher wage around a switch point. This example is not yet sufficient to demonstrate that the economic life of a machine is independent of measures of capital-intensity, as used in mainstream marginalist economics.