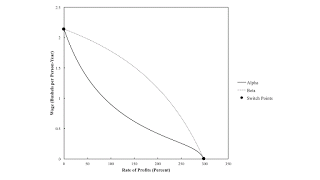
Figure 1: Wage Curves for a Reswitching Example1.0 Introduction This post illustrates another fluke case. In this example economy, two techniques exist for producing a net output of corn. The wage curves for the two techniques have two switch points. One switch point is on the wage axis, corresponding to a rate of profits of zero. The other is on the axis for the rate of profits, corresponding to a wage of zero. This example is a fluke in two ways. In the jargon I have been inventing, it is simultaneously a pattern across the wage axis and a pattern over the axis for the rate of profits. It differs from this previous example in that the switch points in both patterns arise for the same pair of techniques. In my jargon, it is a global pattern. I created this example by simplifying
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics, Sraffa Effects
This could be interesting, too:
Robert Vienneau writes Austrian Capital Theory And Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes Double Fluke Cases For Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes The Emergence of Triple Switching and the Rarity of Reswitching Explained
Robert Vienneau writes Recap For A Triple -Switching Example
|
| Figure 1: Wage Curves for a Reswitching Example |
This post illustrates another fluke case. In this example economy, two techniques exist for producing a net output of corn. The wage curves for the two techniques have two switch points. One switch point is on the wage axis, corresponding to a rate of profits of zero. The other is on the axis for the rate of profits, corresponding to a wage of zero.
This example is a fluke in two ways. In the jargon I have been inventing, it is simultaneously a pattern across the wage axis and a pattern over the axis for the rate of profits. It differs from this previous example in that the switch points in both patterns arise for the same pair of techniques. In my jargon, it is a global pattern.
I created this example by simplifying and perturbing this one.
2.0 The ModelAs usual, managers of firms know of a number of production processes (Table 1). A single commodity - a ton iron, a ton steel, or a bushel corn in the example - is the output of each process. Each process lasts a year and exhibits constant returns to scale. Inputs are defined in physical units, as indicated in the column for the iron-producing process. All inputs are used up in production; there is no fixed capital or joint production.
| Input | Iron Industry | Steel Industry | Corn Industry | |
| Alpha | Beta | |||
| Labor | 1/3 Person-Yr. | 1/2 | 0.061628 | 0.420472 |
| Iron | 1/6 Ton | 1/200 | 1 | 0 |
| Steel | 1/200 Ton | 1/4 | 0 | 0.070079 |
| Corn | 1/300 Bushel | 1/300 | 0 | 0 |
Two techniques are available. The Alpha technique consists of the iron-producing process, the steel-producing process, and the corn-producing process labeled Alpha. The Beta technique consists of same iron-producing and steel-producing processes, with the corn-producing process replaced by the one labeled Beta.
The choice of technique in a capitalist economy is assumed here to be based on cost-minimization for prices of production. Prices of production, for each technique, are characterized by a system of three equations in which the same rate of profits is earned in all three industries, for the processes comprising the technique. I assume that labor is advanced, and wages are paid out of the surplus. And I take a bushel corn as the numeraire.
Under these assumptions, one can draw the wage curve for each technique, as in Figure 1. The outer frontier of the wage curves illustrates the cost-minimizing technique. In the example, the Beta technique is cost-minimizing whatever the distribution of income. It is not uniquely cost-minimizing, however, for the switch points. In the two cases of a zero rate of profits and a wage of zero, any linear combination of the two techniques is cost-minimizing.
3.0 ConclusionSuppose the coefficients of production for the corn-producing process in the Alpha technique were slightly higher. Then no switch points would exist, and the Beta technique would be uniquely cost-minimizing, whatever the distribution of income between wages and profits. The coefficients in the example illustrate a boundary case, just as technical progress creates a situation where prices of production arise for a case of reswitching. If technical progress were to decrease the coefficients of production for the Alpha process, the switch points would be closer together and further from the axes. It might be that what I am now calling a reswitching pattern might never occur. Some other processes for producing iron or steel might supplant the ones in the example, like in this previous example.
 Heterodox
Heterodox
