Heterodox
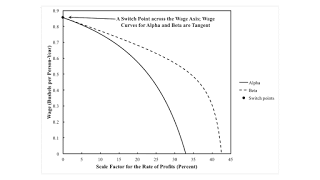
Figure 1: A Switch Point On The Wage Frontier with Wage Curves Tangent This post extends the example in my article in Structural Change and Economic Dynamics, suitably emended. Figure 2 shows an enlargement of part of the parameter space. The parameters of the point where the boundaries of Regions 1, 2, and 3 intersect are shown. In Region 1, the Beta technique is uniquely cost-minimizing for all feasible wages; there are no switch points. Region 2 is a reswitching example, with Beta cost-minimizing at low and high wages. One switch point exists in Region 3, with the Beta technique cost-minimizing at low wages. Figure 2: Part of Parameter Space The boundary between Regions 1 and 2 is tangent to the boundary between Regions 1 or 2 and Region 3. In what I am calling a reswitching
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics, Sraffa Effects
This could be interesting, too:
Robert Vienneau writes The Production Of Commodities And The Structure Of Production: An Example
Robert Vienneau writes A Derivation Of Prices Of Production With Linear Programming
Robert Vienneau writes Reswitching Pattern In Corn-Tractor Model
Robert Vienneau writes Goal: Perturb Special Case Of Steedman’s Corn-Tractor Model
|
| Figure 1: A Switch Point On The Wage Frontier with Wage Curves Tangent |
This post extends the example in my article in Structural Change and Economic Dynamics, suitably emended.
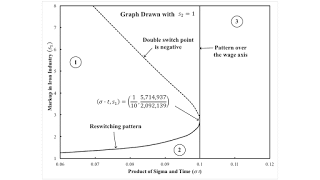
Figure 2 shows an enlargement of part of the parameter space. The parameters of the point where the boundaries of Regions 1, 2, and 3 intersect are shown. In Region 1, the Beta technique is uniquely cost-minimizing for all feasible wages; there are no switch points. Region 2 is a reswitching example, with Beta cost-minimizing at low and high wages. One switch point exists in Region 3, with the Beta technique cost-minimizing at low wages.
|
| Figure 2: Part of Parameter Space |
The boundary between Regions 1 and 2 is tangent to the boundary between Regions 1 or 2 and Region 3. In what I am calling a reswitching pattern, the scale factor for the rate of profits is found as a double root for a polynomial equation. I have extended the boundary between Regions 1 and 2, with the dotted line, to show where this double root occurs with a negative scale factor for the rate of profits.
Figure 1, at the top of this post, shows wage curves for the example for the parameter values noted in Figure 2. (I used Octave to help with my arithmetic.) The Beta technique is cost-minimizing for all feasible wages. When the wage is at its maximum, the Alpha technique is also cost minimizing. And, at the switch point, the two wage curves are tangent. This is a fluke switch point twice over.
This sort of fluke switch point cannot be expected to be found in empirical data from, say, National Income and Product Accounts. The fluke cases I have been developing are important in that they illustrate partitions in a parameter space for certain models of the choice of technique. They arise as certain characteristics of markets vary with a perturbation of model parameters.
I am not sure what to make of structures within the parts of the parameter space I have been exploring. If you think about, you can see why that must be a point of tangency in Figure 2. Maybe the most striking structure I have found is parallel lines for partitioning a parameter space associated with an example of Harrod-neutral technical change.
I write this stuff as escapism. A lot of economists I build on are in Italy, which is a worrisome place to be these days. I hope you are doing well.