Heterodox
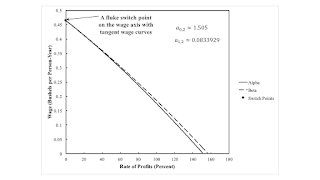
Figure 1: A Wage Frontier With A Fluke Switch Point This post is a rewrite of this, without the attempt to draw a connection to structural economic dynamics. This is the second post in a series, starting with this. A fluke example with fixed capital illustrates the emergence of the reswitching of techniques. Table 1 presents coefficients of production in a perturbation of an example from Schefold (1980). With the first process, workers, under the direction of mangers of firms, manufacture new machines. The remaining two processes are used to produce corn. The last process requires an input of an old machine, which is jointly produced with corn by the second process. Corn is both a consumption good and a capital good, insofar as it is an input into all three processes. Table 1: The
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics, Joint Production, Sraffa Effects
This could be interesting, too:
Robert Vienneau writes The Production Of Commodities And The Structure Of Production: An Example
Robert Vienneau writes A Derivation Of Prices Of Production With Linear Programming
Robert Vienneau writes Reswitching Pattern In Corn-Tractor Model
Robert Vienneau writes Goal: Perturb Special Case Of Steedman’s Corn-Tractor Model
 |
| Figure 1: A Wage Frontier With A Fluke Switch Point |
This post is a rewrite of this, without the attempt to draw a connection to structural economic dynamics. This is the second post in a series, starting with this.
A fluke example with fixed capital illustrates the emergence of the reswitching of techniques. Table 1 presents coefficients of production in a perturbation of an example from Schefold (1980). With the first process, workers, under the direction of mangers of firms, manufacture new machines. The remaining two processes are used to produce corn. The last process requires an input of an old machine, which is jointly produced with corn by the second process. Corn is both a consumption good and a capital good, insofar as it is an input into all three processes.
| Input | Machine Industry | Corn Industry | |
| One Process | Another Process | ||
| Labor | 1/5 | a0,2 | 7/5 |
| Corn | 1/8 | a1,2 | 7/20 |
| New Machines | 0 | 1 | 0 |
| Old Machines | 0 | 0 | 1 |
| Output | |||
| Corn | 0 | 1 | 1 |
| New Machines | 1 | 0 | 0 |
| Old Machines | 0 | 1 | 0 |
The choice of technique corresponds here to the choice of the economic life of the machine. This lifetime is truncated to one year for the Alpha technique, while the machine is operated for its full physical life of two years under the Beta technique. In a pure fixed capital model, the choice of technique can be analyzed by the construction of the wage frontier. The cost-minimizing technique at a given rate of profits has a wage curve on the outer frontier, as illustrated by Figure 1 for a specified parametrization. Managers of firms are willing to operate the machine for two years for any feasible rate of profits. At the maximum wage or a rate of profits of zero, the Alpha technique is also cost-minimizing. The single switch point is a fluke in two ways. First, it lies on the wage axis. Second, the wage curves are tangent at the switch point.
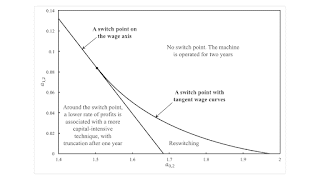
Figure 3 depicts a part of the parameter space for this example. A thin wedge between two partitions extends to the southeast of the point for the parameters corresponding to Figure 1. At the upper edge of this wedge, the two wage curves for the techniques are tangent at a switch point. The example is of reswitching below this partition and within this wedge. At the lower edge of this wedge, the switch point with the lower rate of profits is on the wage axis.
 |
| Figure 2: The Parameter Space for an Example with Fixed Capital |
Reswitching, in this example of fixed capital, is connected to the economic life of a machine. The economic life is the full two years here for a low and high rate of profits. Truncation occurs for a range of intermediate rates of profits. The specification of which technique is cost-minimizing can be consistent with vastly different functional distributions of income, with another technique being cost-minimizing for less extreme distributions
The switch point at the higher rate of profits in the reswitching region of the parameter space illustrates capital-reversing. Around this switch point, a lower rate of profits is associated with the adoption of a less capital-intensive cost-minimizing technique. At any rate of profits, inputs into production in a stationary state can be evaluated at prices of production, and these evaluations can be summed for each technique. The ratio of capital per worker, for example, is an index of the capital intensity of a technique. A more capital-intensive technique produces more output per worker, but its adoption is not necessarily encouraged by a lower rate of profits or interest rate (Harris 1973). In other words, a higher wage is associated with the adoption of a technique that requires a greater input of labor per bushel corn produced net throughout the economy. Capital-reversing has been shown to occur in other examples without reswitching on the wage frontier. Harcourt (1972) surveys the controversy in which economists, such as Paul Samuelson and Robert Solow, in Cambridge, Massachusetts, struggled to accept these conclusions drawn by other economists, such as Joan Robinson and Piero Sraffa, at the University of Cambridge.
Consider the region to the southwest in Figure 2. A single switch point exists on the wage frontier. Around this switch point, a lower rate of profits is associated with the adoption of a technique with a greater value of capital per person-year and a greater output per worker. Nevertheless, truncating the operation of the machine for one year is associated with a more capital-intensive technique. The demonstration of the invalidity of Austrian capital theory does not even need the phenomena of reswitching and capital-reversing.