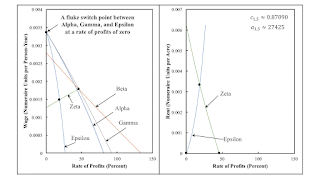
Figure 1: Wage Curves For A Fluke Case1.0 Introduction This post examines perturbations around a fluke case in a model of intensive rent. The model illustrates an analysis of prices and the choice of technique in which the quantity of commodites produced matters. Yet the level and composition of net output are taken as given, independent of any variation, for example, from their dependence on distribution and relative prices. The model also illustrates a case in which prices of production are not uniquely determined by the level of wages. In the fluke case considered, the requirements for use necessitate, for one technique, that the single type of land available be just fully culitivated with a single process being operated. For an infintesimal lower level of output with that
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics, Joint Production, rent
This could be interesting, too:
Robert Vienneau writes Austrian Capital Theory And Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes Double Fluke Cases For Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes The Emergence of Triple Switching and the Rarity of Reswitching Explained
Robert Vienneau writes Recap For A Triple -Switching Example
| Figure 1: Wage Curves For A Fluke Case |
This post examines perturbations around a fluke case in a model of intensive rent. The model illustrates an analysis of prices and the choice of technique in which the quantity of commodites produced matters. Yet the level and composition of net output are taken as given, independent of any variation, for example, from their dependence on distribution and relative prices. The model also illustrates a case in which prices of production are not uniquely determined by the level of wages.
In the fluke case considered, the requirements for use necessitate, for one technique, that the single type of land available be just fully culitivated with a single process being operated. For an infintesimal lower level of output with that technique, the land would be in excess supply, and no rent would be paid. On the other hand, for any increased output, a linear combination of some processes would need to be operated if the given process would be used. The fluke case can be viewed in which two processes are operated on the land, with one process operated at a level of operation of zero. The rent is an additional variable in the equations characterizing prices of production, but, for a given wage, the solution is such that the rent is zero.
The example has a second fluke property. The wage curves for three techniques intersect at a switch point on the wage axis, at a rate of profits of zero.
Perhaps the complexity of this example overwhelms any insight it provides. I expect to continue to explore other areas of the parameter space.
2.0 Technology, Land Endowments, and Requirements for UseThe example varies the parameters from an example by Antonio D'Agata.
Table 1 presents coefficients of production, a perturbation of an example from D'Agata (1983). Only one type of land exists, and three processes are known for producing corn on it. The scarcity of land is shown by the possibility of two corn-producing processes being operated side-by-side in the cost-minimizing technique.
| Input | Industry | ||||
| Iron | Steel | Corn | |||
| I | II | III | IV | V | |
| Labor | 1 | 1 | 1 | 49/25 | 23/25 |
| Land | 0 | 0 | 1 | 9/10 | c1,5 |
| Iron | 0 | 0 | 1/10 | 9/100 | a1,5 |
| Steel | 0 | 0 | 2/5 | 9/100 | 23/250 |
| Corn | 1/10 | 3/5 | 1/10 | 7/25 | 9/25 |
Following D'Agata, assume that one hundred acres of land are available and that net output consists of 90 tons iron, 60 tons steel, and 19 bushels corn. The net output is also the numeraire. All three commodities must be produced for any composition of net output. Table 2 lists the available techniques. Delta is never feasible for the parameter ranges considered. Not all land is farmed and only one corn-producing process is operated under Alpha and Beta. Under Gamma also, only one corn-producing process is operated. Two corn-producing processes are operated together under Epsilon and Zeta.
| Technique | Processes |
| Alpha | I, II, III |
| Beta | I, II, IV |
| Gamma | I, II, V |
| Delta | I, II, III, IV |
| Epsilon | I, II, III, V |
| Zeta | I, II, IV, V |
A set of equations for prices of production can be set out for each technique. Each process in the technique provides one equation. The systems of equations for Alpha, Beta, and Gamma each consist of three equations, and no rent enters into them. The systems for Epsilon and Zeta consist of four equations, with rent as an additional variable. I assume both rent, when it exists, and wages are paid out of the surplus product at the end of the year. The numeraire adds a fourth or fifth equation, depending on the technique.
Given the wage or the rate of profits, these equations can be solved. In the parameter ranges considered, only one solution exists for each technique. Figure 1, at the top of the post, plots wage curves and rent, as a function of the rate of profits, for each feasible technique. In the parameter ranges considered in this post, the wage varies monotonically with the rate of profits for each technique.
Consider the parameters for the fluke case illustrated in Figure 1. For a low wage or a rate of profits higher than the rate of profits at the switch point with the highest rate of profits, the Beta technique is cost-minimizing. The wage curve for Beta contributes to the frontier. Since under Beta, land is in excess supply when the requirements for use are satisfied, no rent is paid if the Beta technique is adopted.
For a higher wage or any non-negative rate of profits up to where the Beta technique is cost-minimizing, the Gamma technique is cost-minimizing. The wage curve for Gamma also contributes to the wage frontier. No rent is paid when the Gamma technique is adopted.
At the maximum wage or a rate of profits of zero, the Alpha technique is cost-minimizing. The wage curve for Alpha contributes to the wage frontier only at the switch point on the wage axis. Land is in excess supply under Alpha, and no rent is paid.
The construction of the wage frontier out of the outer envelope of the wage curves for Alpha, Beta, and Gamma follows the well-known logic of simple (non-joint) production. But this outer envelope is not the entire wage frontier here. The wage curve for Epsilon contributes to the wage frontier between the wage at the switch point between the wage curves for Epsilon and Zeta and the maximum wage. And when Epsilon is adopted, rent is paid, as illustrated on the right pane in Figure 1.
Furthermore, the Zeta technique is also cost-minimizing for a certain range of distribution. Consider the wage at the switch point between Epsilon and Zeta and at the switch point between the wage curves for Beta, Gamma, and Zeta. The wage curve for Zeta contributes to the wage frontier in this range of wages. And rent is paid here too.
So I claim that the choice of technique is not unique for certain ranges of the wage in this fluke case. In an intermediate range of wages, the Beta, Epsilon, and Zeta techniques are each cost-minimizing. Depending on which technique is adopted, a different rate of profits and different prices of production for iron, steel, and corn will prevail. For wages in a range from the upper limit of the previously described range to the maximum wage, the Gamma and Epsilon techniques are cost-minimizing. The rate of profits and prices of production are non-unique here too. If a market algorithm can be defined for this example, what technique and prices of production it would converge to would depend on initial conditions here.
4.0 A Local Partition of the Parameter SpaceI now consider perturbations of the two unspecified coefficients of production in Table 1, around the fluke case illustrated in Figure 1. Further partitions of the parameter space exist outside the borders of Figure 2. But within this plot, the analysis of the choice of technique does not qualitatively vary within each of the four regions.
| Figure 2: A Slice of the Parameter Space around the Fluke Case |
The regions to the northwest and southwest illustrate the analysis of prices of production under simple production. Any of the three corn-producing processes, when combined with the first two processes, can satisfy requirements for use, with some land left over. Land is not scarce, and no technique in which two corn-producing processes operate side-by-side on fully-cultivated land can satisfy requirements for use. The wage frontier, in such a case, is the outer frontier of the wage curves for Alpha, Beta, and Gamma. To the southwest, Beta is cost-minimizing at a low wage, and Gamma is cost-minimizing up to the maximum wage. To the northwest, Alpha is cost-minimizing towards the highest wage.
The Alpha, Beta, Epsilon, and Zeta techniques are feasible in the regions to the northeast and southeast. In the region to the southeast, Beta is cost-minimizing at a low wage. At intermediate wages, Epsilon, Zeta, and Beta are all cost-minimizing. The cost-minimizing technique, the rate of profits, rent, and prices of production are not a unique function of the wage. At a higher wage, up to the maximum wage, Epsilon is uniquely cost-minimizing.
The region to the northeast resembles the region to the southeaqst, except at higher wages. For a range of wages up to the maximum wage, Alpha is uniquely cost-minimizing. No rent is paid on land for a range of low and high wages. But rent can be paid in a range of intermediate wages. In some of this range, where Epsilon is uniquely cost-minimizing, rent must be paid.
5.0 The Choice of TechniqueAbove, I have made many statements about the choice of the cost-minimizing technique. I here briefly describe how you can check these claims.
For each technique and a wage up the maximum wage for that technique, one can find the rate of profits; rent per acre, if any; and prices of production. For each process in Table 1, consider the revenues obtained when producing one ton iron, one ton steel, or one bushel corn, depending on the process. Find the difference between these revenues and costs, where capital goods are costed up at the going rate of profits. This difference, which can be negative, is the extra profits obtained for a given process operated at the unit level, with the prices of production for the given technique at the given wage. These extra profits are always zero for the iron and steel-producing process since equations for these processes enter into the system of equations for prices of production for each technique in the example.
Figure 3 graphs extra profits for the three corn-producing processes for prices of production for the Alpha and Beta techniques. Coefficients of production are as in the fluke case graphed in Figure 1, at the top of this post. You cannot see on the left pane a curve for the third process, that is, the first corn-producing process. This corn-producing process is operated under the Alpha technique, and its extra profits are zero for the full range of possible wages under Alpha. For any wage less than the maximum wage, extra profits can be made by operating the last corn-producing process, and for some range of lower wages, by operating the second corn-producing process. Thus, Alpha is only cost-minizing at the maximum wage, which is a switch point.
| Figure 3: Extra Profits at Alpha and Beta Prices |
The right-pane demonstrates that Beta is cost-minimizing over of range of wages bounded below by zero. If prices of production for Beta prevail and wage exceeds that at the switch point, managers of cost-minimizing farms will want to adopt the last corn-producing processes, sometimes.
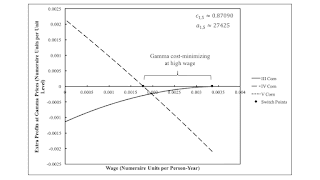
Figure 4 shows extra profits for corn-producing processes when prices of production for Gamma prevail. For the coefficients of production for the fluke case, Alpha, Beta, and Gamma are feasible, and no rent is paid when these techniques are adopted You can see from the graph that Gamma is cost-minimizing over a range of high wages. The maximum wage is at a switch point. Adopting the first corn-producing process at the highest wage will neither incur excess costs or make extra profits.
| Figure 4: Extra Profits at Gamma Prices |
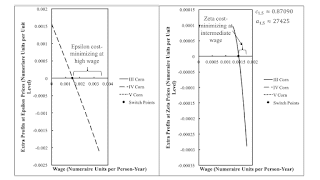
Figure 5 shows extra profits for prices of production for Epsilon and Zeta, respectively. These are the two feasible techniques which pay a rent. Since two corn-producing processes are operated for each of these techniques, a curve showing extra profits is only apparent for one process in each pane. In each case, this is the corn-producing process not operated under the technique for which prices of production are found. Epsilon is only cost-minimizing for a range of the wage up to the maximum wage.
| Figure 5: Extra Profits at Epsilon and Zeta Prices |
Extra profits are only shown in Figure 5 for an intermediate range of wages for Zeta. Below this range, a non-negtive rate of profits cannot be obtained. Above this range, rent must be negative. Zeta is cost-minimizing only in a subrange of high wages for the range of wages in which it makes sense to calculate extra profits for Zeta.
The above has justified the claims in Section 3 about the cost-minimizing technique for the fluke case explored in this post. Parts of the wage curves for the Gamma, Epsilon, Zeta, and Beta techniques lie on the wage frontier for this case. The wage curve for Alpha contributes to the wage frontier only at the switch point at the maximum wage.
6.0 ConclusionOne can think of a movement from the northeast to the southwest in Figure 2 as an example of technical progress. The two coefficients of production I have chosen to explore decrease. As a result of the decline in the acres of land needed to produce corn in one process, land becomes non-scarce for a given net output. Intensive rent disappears.
I think those who have made it this far will grant that the fluke case in Figure 1 is different than any graph of a wage frontier ever seen in the literature. Kurz and Salvadori (1995), for completeness, do consider a case in which requirements for use are satisfied by just cultivating all of a certain type of land. I do not know that any numeric example has ever been put forth where the cost-minimizing technique does not depend uniquely on the wage away from a switch point. But this possibility is known, I guess, to Bidard, Kurz, Salvadori, Schefold, and others. I expect that I may generate further examples in this parameter space.
References- D'Agata, Antonio. 1983. The existence and unicity of cost-minimizing systems in intensive rent theory. Metroeconomica 35: 147-158.
- Kurz, Heinz D. and Neri Salvadori. 1995. Theory of Production: A Long-Period Analysis. Cambridge: Cambridge University Press.
 Heterodox
Heterodox