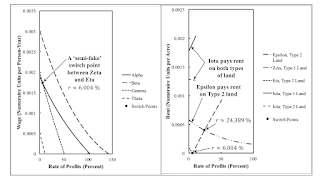
Figure 1: Wage and Rent Curves for a Numeric Example1.0 Introduction This post continues, with some repitition, my exposition of a model of extensive and intensive rent. In the example, the cost-minimizing technique is non-unique at a low enough wage or rate of profits. One cost-minimizing technique, Epsilon, illustrates a case of extensive rent. The other cost-minimizing technique, Iota, illustrates a case with both extensive and intensive rent. In this technique, a kind of absolute rent arises on a land that is only partially farmed, and, thus, in excess demand. The rule of free goods does not seem to apply. (I am not sure how well thought out this idea is.) I also note the existence of what I am calling a 'semi-fake' switch point. The conflicts among workers, landlords, and
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics, rent, Sraffa Effects
This could be interesting, too:
Robert Vienneau writes Austrian Capital Theory And Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes Double Fluke Cases For Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes The Emergence of Triple Switching and the Rarity of Reswitching Explained
Robert Vienneau writes Recap For A Triple -Switching Example
| Figure 1: Wage and Rent Curves for a Numeric Example |
This post continues, with some repitition, my exposition of a model of extensive and intensive rent.
In the example, the cost-minimizing technique is non-unique at a low enough wage or rate of profits. One cost-minimizing technique, Epsilon, illustrates a case of extensive rent. The other cost-minimizing technique, Iota, illustrates a case with both extensive and intensive rent. In this technique, a kind of absolute rent arises on a land that is only partially farmed, and, thus, in excess demand. The rule of free goods does not seem to apply. (I am not sure how well thought out this idea is.) I also note the existence of what I am calling a 'semi-fake' switch point.
The conflicts among workers, landlords, and capitalists are complicated in this example. At a given rate of profits, workers get a lower wage if landlords can get more rent. At a given wage, the rate of profits is lower if landlords can get more rent
Economists demonstrated over a half-century ago that a theory of supply and demand functions is a kind of nonsense.
2.0 TechnologyTable 1 presents coefficients of production for the example. Here, two types of land exist. Only one agricultural commodity, corn, can be produced on the processes in which land is used. For the second type of land, two processes can be operated on land. Only one process is known for producing the industrial commodity.
| Input | Industry | |||
| Iron | Corn | |||
| I | II | III | IV | |
| Labor | a0,1 = 1 | a0,2 = 9/10 | a0,3 = 91/250 | a0,4 = 1/2 |
| Type I Land | 0 | c1,2 = 1 | 0 | 0 |
| Type II Land | 0 | 0 | c2,3 = 13/10 | c2,4 = 1 |
| Iron | a1,1 = 2/5 | a1,2 = 1/50 | a1,3 = 9/10,000 | a1,4 = 67/1000 |
| Corn | a2,1 = 2 | a2,2 = 6/125 | a2,3 = 27/100 | a2,4 = 3/20 |
I assume 300 acres of Type 1 land and 200 acres of Type 2 land are available. Requirements for use, that is, required net output, consists of 90 tons iron and 60 tons steel. This commodity basket is also the numeraire.
Table 2 lists the available techniques of production. Not all are feasible. Feasibility depends on requirements for use (that is, required net output) and how much of each type of land is available. Rent is zero for the Alpha, Beta, and Gamma techniques, since neither type of land is fully used. That is, land is not scarce. Techniques Delta, Epsilon, Zeta, and Eta are examples of extensive rent since only one process is operated on each type of land. The Theta technique resembles an example of intensive rent. Finally, if the Iota technique is adopted, one will observe both extensive and intensive rent.
| Technique | Processes | Type 1 Land | Type 2 Land |
| Alpha | I, II | Partially farmed | Fallow |
| Beta | I, III | Fallow | Partially farmed |
| Gamma | I, IV | Fallow | Partially farmed |
| Delta | I, II, III | Fully farmed | Partially farmed |
| Epsilon | I, II, III | Partially farmed | Fully farmed |
| Zeta | I, II, IV | Fully farmed | Partially farmed |
| Eta | I, II, IV | Partially farmed | Fully farmed |
| Theta | I, III, IV | Fallow | Fully farmed |
| Iota | I, II, III, IV | Partially farmed | Fully farmed |
Under these assumptions, the Delta, Epsilon, Zeta, Eta, and Iota techniques are feasible. The processes in the Alpha, Beta, Gamma, and Theta techniques cannot be operated at any level in which requirements for use are satisfied. Both types of land must be farmed to meet requirements for use.
3.0 The Choice of TechniqueA system of price equations is associated with each technique. Wage curves for the Alpha, Beta, Gamma, and Theta techniques are shown in the left pane of Figure 1 at the top of this post. I only consider, in the analysis of the choice of technique, ranges of the rate of profits in which neither rent nor the wage is negative. This criterion rules out the Delta technique, always. Which type of land is fully farmed varies with which process is chosen for operation on type 2 land.
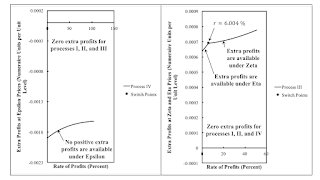
Under Epsilon, process III is operated; Type 2 land is fully farmed; and Type 1 land pays no rent. The Epsilon technique is, in some sense, a combination of the Alpha and Beta techniques. The wage curve for Beta is further out than the wage curve for Alpha wage curve for the full range of profits. The wage curve for Epsilon is the Alpha wage curve, that is the further inward of the Alpha and Beta wage curves. The left pane in Figure 2 shows that Epsilon is cost-minimizing for the full range of the rate of profits in which the wage curve for Alpha is in the first quadrant; extra profits cannot be obtained by operating process IV, the only process not in the Epsilon technique, at Epsilon prices. Thus, the intersections of the Alpha and Gamma wage curves and of the Epsilon and Zeta rent curves are not switch points.
| Figure 2: The Epsilon Technique Is Cost-Minimizing; The Zeta and Eta Techniques Are Never Cost-Minimizing |
The Zeta and Eta techniques are a combination of the Alpha and Gamma techniques. The intersections of the Alpha and Gamma wage curves and the Eta and Zeta rent curves, at a rent of zero, relate to the range of the rate of profits at which they can enter into the analysis of the choice of technique. These intersections occur at the same rate of profits. The wage curves for Zeta and Eta are the innermost frontier of the Alpha and Gamma wage curves. For a rate of profits less than at the semi-fake switch point, Alpha is the frontier. Type 1 land pays no rent, and the Zeta technique cannot be operated with a non-negative rent. For a higher rate of profits, Gamma is the frontier, and Type 2 land pays no rent. Since only two types of land exist in this example, the order of fertility cannot deviate from the order of fertility. The right pane in Figure 2 shows that neither the Zeta nor the Eta technique is ever cost-minimizing.
The Iota technique is, in some sense. a combination of the Alpha and Theta techniques. The price equations for Theta determine, at a given rate of profits, the wage, the prices of corn and iron, and the rent on Type 2 land. Type 2 land is fully farmed under Theta. A linear combination of the price equations for processes III and IV eliminates rent from these equations. One ends up with a system of two price equations, for iron and corn, with one degree of freedom, given the numeraire. But the Theta technique cannot satisfy requirements for use. The price equation for process II, which operates on Type 1 land, can only be satisfied if rent on Type 1 land is positive. It does not matter for this solution whether or not Type 1 land is fully farmed. The wage frontier for Iota is the innermost of the Alpha and Theta wage curves, that is, the Theta wage curve. Since all processes in the example enter into the Iota technique, no extra profits can be obtained by operating any process at Iota prices. Iota is always cost minimizing, up to the maximum rate of profits for the Theta technique. What do you think of this absolute rent on Type 1 land?
So the above presents my rationale for saying this is an example, at low rates of profits, of non-unique cost-minimizing techniques. Prices, including the wage and rents per acre, are also non-unique. And I am able to apply a theory of prices, in an open model, without ever deriving supply and demand functions.
4.0 An Aside on Multiple Agricultural CommoditiesI do not know if, for example, the possibility of absolute rent, with some land of a specified quality left uncultivated has been noticed before.
I also think the following claim, from the chapter on rent in Piero Sraffa's PofCbyMofC, has not been justified or falsified in non-fluke cases:
"89. More complex cases can generally be reduced to combinations of the two that have been considered. The main type of complication arises from the multiplicity of agricultural products.
Thus, suppose that in the first case land of one quality was so exceptionally well-suited for one particular crop, that such a crop was grown on the whole of that land and on no other land; under these circumstances there would be room for two different methods of producing the crop in question on that land, and its rent would be determined independently of that of the other lands becoming in effect an instance of the second case.
Or consider the more general case in which each of several qualities of land can be used for several alternative crops; although none of the crops is grown on land of all qualities; while on the other hand none of the lands is sufficiently specialised to have its rent determined independently of the others. What is required in any case is that the number of separate processes should be equal to the number of qualities of land plus the number of products concerned; and, moreover, that the links or overlaps between the various products and the various lands on which they are grown should be sufficient for the determination of the rents and the prices. The type of link required may be sufficiently indicated by the consideration that the above condition were such as to make possible the construction of a Standard commodity from which were excluded all the lands as well as any non-basics among the products.
In the case of a single quality of land, the multiplicity of agricultural products would not give rise to any complications. It may however be noted that only for one of the crops would two separate methods of production be compatible; for the rest, the number of processes would have to be equal to the number of products." Sraffa (1960)
Sraffa certainly does not justify that claim in his book. I suppose I could work through the example problems at the end of Chapter 10 of Kurz and Salvador (1995) and look up the authors from which these examples are drawn. These authors include Antonio D'Agata, Guido Erreygers, Giuseppe, Alberto Quadrio-Curzio, and Philippe Saucier. Unfortunately, a lot of this work seems to be languages I cannot read.
 Heterodox
Heterodox