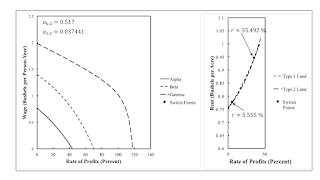
Figure 1: An Example of the Reswitching of the Order of Rentability1.0 Introduction Nobody has ever pointed out the possibility highlighted by this post, as far as I know. Talk of "switch points" and "reswitching" for the rent curves on the right pane in Figure 1 above is an abuse of terminology. Under capitalism, land obtains rent because land is scarce. The power of the state backs up individuals prohibiting others from using free gifts of nature. (Propertarians are about encouraging government intervention in the economy.) Consider a system of prices of production, given the rate of profits. Whether or not a type of land receives a rent can vary with the rate of profits. Suppose two landlords own different kinds of land, both of which obtain rent. Who receives more rent per acre
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics, Joint Production, Sraffa Effects
This could be interesting, too:
Robert Vienneau writes Austrian Capital Theory And Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes Double Fluke Cases For Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes The Emergence of Triple Switching and the Rarity of Reswitching Explained
Robert Vienneau writes Recap For A Triple -Switching Example
| Figure 1: An Example of the Reswitching of the Order of Rentability |
Nobody has ever pointed out the possibility highlighted by this post, as far as I know. Talk of "switch points" and "reswitching" for the rent curves on the right pane in Figure 1 above is an abuse of terminology.
Under capitalism, land obtains rent because land is scarce. The power of the state backs up individuals prohibiting others from using free gifts of nature. (Propertarians are about encouraging government intervention in the economy.)
Consider a system of prices of production, given the rate of profits. Whether or not a type of land receives a rent can vary with the rate of profits. Suppose two landlords own different kinds of land, both of which obtain rent. Who receives more rent per acre can also vary with the rate of profits.
This post presents a numerical example of extensive rent in which the order of fertility does not vary with distribution. Wage curves do not intersect. That is, there are no switch points. Yet the ranking of lands by rent per acre varies with distribution. The same order of rentability appears at low and high rates of profits, with a different order arising for intermediate rates of profits.
2.0 TechnologyThe analysis of the choice of technique in models of extensive rent can be based on the construction of wage curves, even though the outer envelope does not represent the cost-minimizing technique. The orders of fertility and rentability are emphasized here. The order of fertility is defined for specified techniques, in which multiple qualities of land are used in each technique, and a single quality of land pays no rent. At a given rate of profits, the qualities of land are ordered by wages, with the most fertile land paying the highest wage. The order of rentability specifies the sequence of different qualities of lands from high rent per acre to low rent per acre. Both orders may vary with the wage or the rate of profits. Table 1 presents coefficients of production for an example.
| Input | Iron Industry | Corn Industry | ||
| I | II | III | IV | |
| Labor | 1 | a0,2 | 91/250 | 67/100 |
| Type 1 Land | 0 | 49/100 | 0 | 0 |
| Type 2 Land | 0 | 0 | 59/100 | 0 |
| Type 3 Land | 0 | 0 | 0 | 9/20 |
| Iron | 9/20 | a1,2 | 9/10000 | 67/1000 |
| Corn | 2 | 6/125 | 27/100 | 3/20 |
The amount of corn that can be produced is constrained by the available quantities of each type of land. Endowments of land and requirements for use must be among the givens to analyze the choice of technique in this example. Suppose the quantities of the different types of land and net output is such that all three types of land must be farmed. One type will be only partially farmed. The iron-producing process must be operated in each of the three economically viable techniques. Table 2 describes which type of lands are fully cultivated and which type of land is left partially fallow in each of the Alpha, Beta, and Gamma techniques.
| Technique | Land | ||
| Type 1 | Type 2 | Type 3 | |
| Alpha | Fully farmed | Fully farmed | Partially farmed |
| Beta | Partially farmed | Fully farmed | Fully farmed |
| Gamma | Fully farmed | Partially farmed | Fully farmed |
Figure 1 shows three wage curves on the left pane in Figure 1. The parameters a0,2 and a1,2 are as specified. The wage and price of iron are found, for each technique, as functions of the rate of profits. These functions are found by solving a system of two linear equations, given the rate of profits and the specification of a bushel corn as numeriare.
3.1 The Price System for A TechniqueThe process for producing iron contributes the following equation for the price system:
((9/20) p + 2)(1 + r) + 1 w = p
where p is the price of a ton of iron, r is the rate of profits, and w is the wage for a person-year of labor. I assume wages and rent is paid out of the surplus product at the end of the year.
The second equation comes from the process for producing corn on the type of land that is only partially farmed. This is Type 3 land for the Alpha technique. No rent appears in this equation, since Type 3 land is not scarce:
((67/100) p + (3/20))(1 + r) + (67/100) w = 1
The two equations, given the rate of profits, is a system of two equations in two unknowns, the price of iron and the wage. A solution exists, with a positive price of iron and a positive wage exists for a nonegative rate of profits up to a maximum associated with the technique. The wage curve on the left pane in Figure 1, labeled "Alpha", shows the solution to this system for wages.
Rent must be such that processes operated on lands that are fully farmed make the same rate of profits as the type of land that is not scarce. For the Alpha technique, Type 1 land contributes the following equation:
(a1,2p + (6/125))(1 + r) + (49/100) ρ1 + a0,2w = 1
where ρ1 is rent per acre for Type 1 land. Given the parameters for the coefficients of production, the rate of profits, and the solution for the system of two equations for the price of iron and the wage, the rent per acre ρ1 is the only unknown in this equation.
Tpe 2 land, for the Alpha technique, contributes the following equation:
((9/10000) p + (27/100))(1 + r) + (59/100) ρ2 + (91/250) w = 1
where ρ2 is rent per acre for Type 2 land. Here, too, rent per acre is the only remaining unknown. For any rate of profits that yields a non-negative wage for the Alpha technique, rent per acre for Type 1 and Type 2 lands is positive.
Rent per acre, as functions of the rate of profits, is shown for Type 1 and Type 2 land in the right pane in Figure 1. These functions are for the Alpha technique. These two rent curves intersect twice. The order of lands, from high to low rent per acre, varies with the rate of profits. Notice that no quantity flows vary, in this example, with the variation in the order of rentability. For any feasible distribution of income, Type 1 and Type 2 lands are fully farmed. The number of acres of Type 3 land that are left fallow also does not vary. Prices are are all that varies. Since quaqntity flows do not vary, I am abusing language by calling these intersections of rent curves "switch points". I, however, do not have another technical term available.
3.1 The Choice of TechniqueThe managers of firms choose among techniques on the basis of cost, where the prices must be such that no land pays a negative rent.
At a given rate of profits, order the wage curves on the left pane in Figure 1 from high wages to low wages. This is the order of fertility. Suppose the Gamma technique were adopted. Type 2 land would pay no rent. But Type 1 and Type 3 lands would pay negative rent per acre at the wage appropriate for the Gamma technique. So this technique cannot be cost-minimizing.
Suppose, instead, the Beta technique is adopted. Then, Type 2 land has positive rent per acre, and Type 3 land requires a negative rent per acre. Beta is not cost-minimizing either.
In this example, the Alpha technique is always cost-minimizing. Given the rate of profits, one works down among wage curves from high wages to low wages until one finds the wage curve for a technique at which requirements for use can be satisfied by cultivating only lands that obtain a non-neagtive rent. In the example, in which all three types of land must be cultivated, at least somewhat, the inner frontier is the wage curve for the cost-minimizing technique.
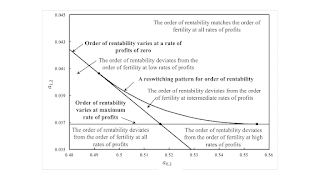
4.0 Perturbation of Selected ParametersFigure 2 shows a partition of part of the parameter space around the example illustrated in Figure 1. No switch points exist for any regions in this small two-dimensional slice of the parameter space. The wage curves do not intersect, and the order of fertility is such that Type 2 land is more fertile than Type 1 land for any income distribution. Type 3 land pays no rent.
| Figure 2: A Portion of the Parameter Space |
The example illustrated is for parameters in the central region in Figure 2. Here, the order of rentability varies from the order of fertility at intermediate rates of profits, but not for low and high rates of profits. This intermediate region disappears at the partition between this central region and the region to the northeast. The two curves for rent on the right in Figure 1 become tangent at a single rate of profits for points along this partition. Consequently, the order of rentability is identical to the order of fertility for any parameters in the region to the northeast.
The two curves for rent intersect at single point for parameters in the regions to the west and the southeast in Figure 2. The order of rentability deviates from the order of fertility for low rates of profits in the region to the west. In the region to the southeast, the order of rentability differs from the order of fertility for high rates of profits.
The two curves for rent do not intersect at all for parameters in the region to the southwest. The order of rentability differs from the order of rentability for any feasible rate of profits in this region. This exploration of the parameter space is only a local perturbation. Results for the analysis of the choice of technique are qualitatively quite different in other parts of the parameter space.
5.0 ConclusionThe order of fertility can vary with the wage or the rate of profits. The order of rentability can also vary with the wage or the rate of profits. And they can vary from one another with distribution. The rate of fertility may vary may vary with distribution, while the order of rentability stays constant. Or the order of rentability may vary with distribution, as in this post, while the order of fertility stays constant. And both of these variations with distribution may be non-monotonic, as in reswitching of techniques.
The reswitching of the order of rentability is not a fluke case. I do not think this example would surprise, for example, Heinz Kurz, Neri Salvadori, or Fabio Petri. Nevertheless, I think nobody has explicitly pointed out this possibility. Is this example "perverse" from the viewpoint of obsolete marginalist economics?
 Heterodox
Heterodox