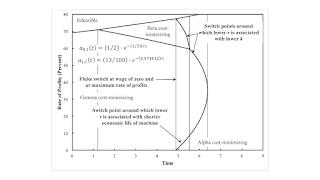
Figure 1: Variation of Switch Points with Technological Progress in Industry This post is an expansion on this post. Technological progress in industry, in which the machine is produced, can be illustrated in Figure 1 in the previous post by a movement roughly from off the graph to the upper right to below the lower left. More concretely, suppose each of the two non-zero coefficients of production in the machine industry decrease at a constant rate of σ0 and σ1 respectively. The two coefficients of production thus vary with time as an exponential function. Variation in the efficiency of the machine with age in agriculture is unaffected by this technological progress in industry. One can calculate prices of production, including switch points, at each instant of time. The machine does
Topics:
Robert Vienneau considers the following as important: Austrian School Of Economics, Example in Mathematical Economics, Joint Production
This could be interesting, too:
Robert Vienneau writes Austrian Capital Theory And Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes Double Fluke Cases For Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes The Emergence of Triple Switching and the Rarity of Reswitching Explained
Robert Vienneau writes Recap For A Triple -Switching Example
| Figure 1: Variation of Switch Points with Technological Progress in Industry |
This post is an expansion on this post.
Technological progress in industry, in which the machine is produced, can be illustrated in Figure 1 in the previous post by a movement roughly from off the graph to the upper right to below the lower left. More concretely, suppose each of the two non-zero coefficients of production in the machine industry decrease at a constant rate of σ0 and σ1 respectively. The two coefficients of production thus vary with time as an exponential function.
Variation in the efficiency of the machine with age in agriculture is unaffected by this technological progress in industry. One can calculate prices of production, including switch points, at each instant of time. The machine does not work with a constant efficiency throughout its physical life. The inputs of seed corn needed to work with the machine increase in agriculture as the machine ages. Labor inputs first increase and then decrease. Whether a two-year old machine is more efficient than a three-year old machine cannot be determined based on physical data alone.
| Figure 2: Variation of Switch Points and Wages with Technological Progress in Industry |
Figure 1 plots the maximum rate of profits and the rate of profits for switch points against time, for specified parameters for technological progress. Figure 2 shows the corresponding plot with the wage as the ordinate. Progress in industry manifests in the variation in the economic life of the machine, as it is used in agriculture. At the start, the machine is used for its full three years, whatever the distribution of income. It is used for only one year, whatever the distribution, at the end of the technological progress depicted here. Switch points, including so-called ‘perverse’ switch points arise during this process, but eventually vanish.
The vertical partitions in the figures occur at times in which at least one switch point is a fluke. The illustrated fluke cases are for a switch point arising at a rate of profits of zero, switch points at the maximum rate of profits, a switch point in which three wage curves intersect, and a switch point in which two wave curves are tangent. The rate of decrease of corn inputs per produced machine has been carefully chosen to ensure the occurrence of the fluke case illustrated in Figure 2 in the previous post. Generally, the fluke case in which the switch point between Alpha and Beta occurs at the maximum rate of profits will occur before or after the fluke case in which a switch point between Alpha and Gamma occurs at the maximum wage. One cannot expect technology to evolve such that two fluke cases occur simultaneously.
A fluke case is such that almost any perturbation of model parameters disturbs its qualitative properties. Between fluke cases, the number and sequence of switch points along the wage frontier, as depicted in Figures 1 and 2, are invariant. This perturbation analysis illustrates that switch points with positive real Wicksell effects are not fluke cases. Likewise, associations of a shorter economic life of a machine with greater capital intensity or with a lower rate of profits are not fluke cases. Heterodox
Heterodox