Figure 1: Wage Curves for the Two Techniques1.0 Introduction Economists following the Austrian school often represent the structure of production with Hayekian triangles (Hayek 1931, Rothbard 1962, Skousen 1990, Garrison 2001, Machaj 2017). Typically, goods of the highest order are produced with unaided labor or other unproduced original resources. (Fillieule (2007), in which a Hayekian triangle is constructed with an infinite stream of unproduced inputs, is an exception.) Rarely, is a model of the production of commodities by means of commodities, as in Sraffa (1960), considered. This post illustrates how to construct a Hayekian triangle with such a model, in the case with circulating capital. It also illustrates how the use of such triangles to tell the stories that Austrian
Topics:
Robert Vienneau considers the following as important: Austrian School Of Economics, Example in Mathematical Economics
This could be interesting, too:
Robert Vienneau writes Austrian Capital Theory And Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes Double Fluke Cases For Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes The Emergence of Triple Switching and the Rarity of Reswitching Explained
Robert Vienneau writes Recap For A Triple -Switching Example
| Figure 1: Wage Curves for the Two Techniques |
Economists following the Austrian school often represent the structure of production with Hayekian triangles (Hayek 1931, Rothbard 1962, Skousen 1990, Garrison 2001, Machaj 2017). Typically, goods of the highest order are produced with unaided labor or other unproduced original resources. (Fillieule (2007), in which a Hayekian triangle is constructed with an infinite stream of unproduced inputs, is an exception.) Rarely, is a model of the production of commodities by means of commodities, as in Sraffa (1960), considered. This post illustrates how to construct a Hayekian triangle with such a model, in the case with circulating capital.
It also illustrates how the use of such triangles to tell the stories that Austrian economists want to tell cannot be sustained.
This post uses one special case to consider another. A model of the production of commodities with only circulating capital and one original factor of production, labor, is used to examine Hayekian triangles, which cannot be rigorously constructed in more general cases (Hayek 1941). This approach is consistent with the research strategy recommended by Harwick (2022). Harwick's argues that capital theory needs to consider exemplary special cases, not begin with the most general case. Here, the most general cases would be general joint production and flow-input, flow-output models. (Hayek 1941 seems to be the source for the classification of inputs as point input or flow input and outputs as point output or flow output.)
Other approaches to capital theory by economists following the Austrian school, such as the use of the financial measure of Duration by Lewin & Cachanosky (2021), are not treated in this post. Fratini (2019) criticizes this financial approach, approach based on reswitching.
2.0 Technology and Net OutputSuppose technology is as characterized by the coefficients of production in Table 1. All techniques are characterized by single production, no fixed capital, and no joint production. In the Alpha technique, the first corn-producing process is operated. The second corn-producing process is operated in the Beta technique. The ale-producing process is operated in both techniques.
| Input | Corn Industry | Ale Industry | |
| Process I | Process II | Process III | |
| Labor | 1 person-yr. | 275/464 person-yrs. | 1 person-yr. |
| Corn | 1/10 kilo-bushels | 113/232 kilo-bushels | 2 kilo-bushels |
| Ale | 1/40 kilo-liters | 1/800 kilo-liters | 2/5 kilo-liters |
| OUTPUTS | 1 kilo-bushel | 1 kilo-bushel | 1 kilo-liter |
Each column in the Leontief matrix and corresponding direct labor coefficient defines a production process. Each process exhibits constant returns to scale and requires a year to complete. Each of the produced commodities are available at the end of the year. All commodities enter, either directly or indirectly, into the production of all commodities and the economy is productive. Labor is directly required to operate each process.
This analysis takes the proportions in the net product as given. These proportions are specified by a column vector, as in Table 2. This numeraire is the net product or net output of Sraffa's standard system for the Alpha technique. This special case has implications for the shape of Hayekian triangles, as seen below.
| Commodity | Amount |
| Corn | d1 = (337 - 29 (29)1/2)/455 kilo-bushels |
| Ale | d2 = (17 + 25 (29)1/2)/1,820 kilo-kiters |
The capital goods required as inputs are found by solving the model. The money supply is here assumed to adjust as needed. The construction of a traverse from one equilibrium to another is a difficult question. In a disequilibrium process, one would need to consider disappointed expectations and inconsistent plans, for example. Mainstream economists have a theory of non-steady state equilibrium paths. Rosser (1983) argues that reswitching manifests as a cusp catastrophe in this theory. Gram & Harcourt (2017) note some issues raised by taking the theory of equilibrium paths as an answer to the reswitching controversy. In the theory, any time to get into equilibrium is too long.
The numeric example is constructed on the basis of the following assumptions, in addition to those already given for characterizing the available technology:
- Stationary states are compared.
- Only one original factor of production, labor, is used.
- One person-year is employed. More generally, full employment is assumed, with a given size of the labor force.
- Wages are paid at the end of the year, not advanced with the payments for capital goods at the beginning of the year.
Hayekian triangles cannot be constructed under the more general assumptions of Hayek (1941).
3.0 Price SystemsPrices and distribution are specified with one degree of freedom, by a given technique. Prices must satisfy the following equations, given the technique, for the same rate of profits to be obtained in both industries:
(p1a1,1 + p2a2,1)(1 + r) + w a0, 1 = p1
(p1a1,2 + p2a2,2)(1 + r) + w a0, 2 = p2
The following equation follows from the definition of the numeraire.
p1d1 + p2d2 = 1
Adam Smith called these prices 'natural prices'. David Ricardo called them 'prices of production'. Alfred Marshall called them 'normal prices'. At any rate, they define the appropriate price system for an economy in a synchronized state, as in this thought experiment.
The model in this article is open. Distribution, including the wage and the interest rate, are not determined. Dumenil & Levy (1985) present a model in which workers consume their entire wage and the interest rate varies with shifts in the capitalists' utility functions. Marglin (1984) also presents a model with intertemporal utility maximization, as well as non-neoclassical ways of closing the model. Closures with intertemporal utility maximization can explain how the interest rate varies. Multiple equilibria can arise in such models.
Figure 1 shows the wage curves for the two techniques. The choice of the numeraire results in the wage curve for the Alpha technique being a straight line, that is, an affine function. Look at the intercepts on the abscissa. The maximum rate of profits for the Beta technique exceeds the maximum for the Alpha technique. On the other hand, the intercepts on the ordinate show that net output per worker for the Beta technique exceeds the net output per worker for the Alpha technique. If the curvature for the wage curve for the Beta technique were concave to the origin, these properties of the intercepts would be reversed in a reswitching example.
The analysis of the choice of technique, in the circulating capital case, does not rely on the construction of the so-called factor price frontier. Milano (2024) notes that this is a misleading name for the wage frontier in Figure 1. Rather, this analysis has an algorithmic justification in the analysis of prices of production (Bharadwaj 1970, Woods 1990, Bidard 1990, Vienneau 2005 and 2017). Bidard & Klimovsky (2004) that the analysis based on the wage frontier does not necessarily extend to general joint production. Specific analyses have been developed for special cases of joint production, notably in the case of fixed capital and of extensive and intensive rent (Pasinetti 1980).
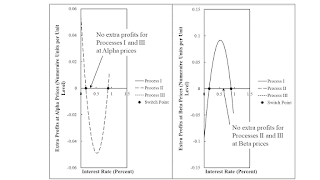
Figure 2 illustrates another analysis of the cost-minimizing technique. The left-hand side is constructed with prices for the Alpha technique, while the right-hand side illustrates prices for the Beta technique. One can see that greater profits are obtained, at low and high rates of profits, by adopting the second corn-producing process at Alpha prices. Likewise greater profits are obtained, at intermediate rates of profits, by adopting the first corn-producing process at Beta prices. Thus, the cost-minimizing technique, at a given interest rate, is the technique contributing its wage curve to the outer frontier at that interest rate.
| Figure 2: Extra Profits for Price Systems |
This example can be used to explore two parables, what one might call a neoclassical and a Austrian story:
- A lower interest rate incentivizes managers of firms to adopt a more capital-intensive technique. With more capital per worker, the steady-state net output per worker is higher.
- A lower time preference results in a willingness to defer consumption and a lower interest rate. This lower time preference is seen in the support of a longer structure of production and less consumption per worker.
The second switch point demonstrates that the first story is ill-founded. The construction of Hayekian triangles below demonstrates the second story is ill-founded. The example does demonstrate that the second story is not refuted merely by objections to the first.
4.0 Perverse Hayekian Triangles at the First Switch PointIn a previous post, I showed how to find the labor used to produce net output, in the current and each future year, when production is synchronized in a given year.
The increment in each step, for a given technique, is the value added by the original factors of production in that step. That is, an increment is the product of the wage and the labor for that order of goods, properly costed up with interest charges.
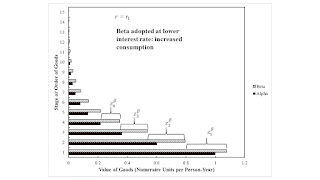
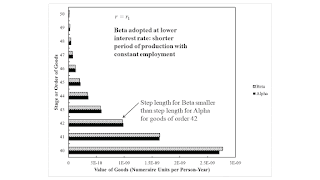
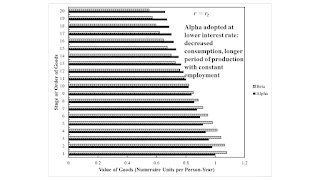
Figures 3 and 4 display the Hayekian triangles at the first switch point. The ordinate is the order of goods, as in Menger (187?). The abscissa is the value of the goods of that order that ultimately go into producing consumption goods, that is, goods of the first order. The length of the first step is the intersection of the corresponding wage curve with the ordinate in Figure 1. The increments in the steps are the values added by original, unproduced factors of production. In this case, labor is the only original factor of production.
| Figure 3: Hayekian Triangle at First Switch Point |
| Figure 4: Hayekian Triangle at First Switch Point for Goods of Higher Order |
Notice that the step for goods of first order is longer for the Beta technique. For goods of order 42 and higher, the step for the Alpha technique is higher. Since Beta is cost-minimizing at a lower interest rate around this interest rate, a lower interest rate is associated with the adoption of a shorter structure of production to produce more goods of the first order. This effect is perverse from the perspective of the Austrian story that Hayek developed his triangles to illustrate.
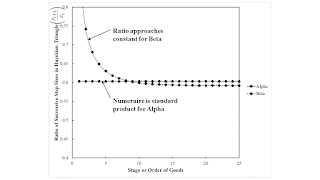
One can look at the ratio of successive increments of step sizes in these Hayekian triangles (Figure 5). This ratio is a constant for the Alpha technique. Because of the composition of the consumption good, this ratio does not vary with the order of goods. This ratio, for the Beta technique, approaches a constant as the order of goods increases without bound. Under the assumptions in which a Hayekian triangle can be constructed from a model of the production of commodities, this ratio always approaches a limiting value. This limit increases with the interest rate for which the triangle is constructed. It is smaller for a larger maximum interest rate. Since the intersection of the wage curves with the abscissa in Figure 1 is larger for Beta, the structure of production for Alpha is ultimately longer in Figure 4.
| Figure 5: Ratios of Value Added at First Switch Point |
One can also consider Hayekian triangles at the second switch point (Figure 6). This switch point is perverse from the perspective of neoclassical theory. Around this switch point, the Alpha technique is cost-minimizing at a lower switch point. The Alpha technique has a longer structure of production and produces less goods of the first order. This pivoting of the structure of production is just the story that Hayek invented his triangles to tell.
| Figure 6: Hayekian Triangle at Second Switch Point |
"While the controversy about public works was developing, Professor Robbins sent to Vienna for a member of the Austrian school to provide a counter attraction to Keynes. I very well remember Hayek's visit to Cambridge on his way to the London School. He expounded his theory and covered a black board with his triangles. The whole argument, as we could see later, consisted in confusing the current rate of investment with the total stock of capital goods, but we could not make it out at the time. The general tendency seemed to be to show that the slump was caused by [excessive] consumption. R. F. Kahn, who was at that time involved in explaining that the multiplier guaranteed that saving equals investment, asked in a puzzled tone, 'Is it your view that if I went out tomorrow and bought a new overcoat, that would increase unemployment?' 'Yes,' said Hayek, 'but,' pointing to his triangles on the board, 'it would take a very long mathematical argument to explain why.'" -- Joan Robinson. 1972. The second crisis of economic theory.Conclusion
The above has analyzed a reswitching example, with two techniques, in a model of the production of commodities by means of commodities. The switch point that is normal, from a mainstream neoclassical perspective, has perverse Hayekian triangles. The switch point that is perverse from a mainstream perspective has Hayekian triangles consistent with the Austrian story about how an increased time preference rotates the triangle to lengthen the structure of production. If the wage curve for Beta were concave to the origin, on the other hand, the first, normal switch point would also be normal from an Austrian perspective, and the second switch point would be perverse from both a neoclassical and Austrian perspective. But what would happen if only one or three switch points existed? Hayekian triangles cannot both be made rigorous and sustain an Austrian story on capital theory.
On the other hand, this post has shown that Austrian economists are correct to claim to have some perspectives distinct from mainstream economists. A refutation of tradional neoclassical capital theory is not, by itself, sufficient to refute all varieties of Austrian capital theory. Furthermore, the analysis in this post has illustrated that, in a model of the production of commodities, the ratio of step sizes in Hayekian triangles approaches a constant (as in Fillieule 2007), dependent on the interest rate for which the triangles are drawn and the maximum interest rate.
This post has drawn no conclusions about monetary theory or macroeconomics. Economists from the Austrian school often draw on capital theory for such purposes. Capital theory can hardly be radically modified without further consequences. Considering such consequences, however, has been on the agenda since Hayek (1941).
 Heterodox
Heterodox