Heterodox
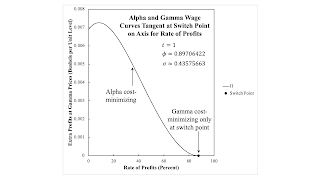
Figure 1: Extra Profits at Gamma Prices for the Second Double-Fluke Switch Point This post is a continuation of this series of posts. A switch point in which wage curves are tangent on the axis for the rate of profits is a double-fluke case symmetrical to the double-fluke case in the previous post. As shown in Figure 1, this case arises in this example as well. The roles of the Alpha and Gamma techniques are reversed. Alpha is always cost-minimizing, while Gamma is cost-minimizing only at the switch point. This symmetry extends to partitions of the parameter space, as seen in Figure 2. A locus corresponding to a switch point at which wage curves are tangent bounds a region, 1 or 4, in which no switch points exist. Reswitching occurs in regions 3 and 5, which are on the other side of
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics
This could be interesting, too:
Robert Vienneau writes A Double-Fluke Switch Point For A Triple-Switching Example
Robert Vienneau writes A 1D Diagram For A Triple-Switching Example
Robert Vienneau writes Three Examples For The Cambridge Capital Controversy
Robert Vienneau writes The Production Of Commodities And The Structure Of Production: An Example
 |
| Figure 1: Extra Profits at Gamma Prices for the Second Double-Fluke Switch Point |
This post is a continuation of this series of posts.
A switch point in which wage curves are tangent on the axis for the rate of profits is a double-fluke case symmetrical to the double-fluke case in the previous post. As shown in Figure 1, this case arises in this example as well. The roles of the Alpha and Gamma techniques are reversed. Alpha is always cost-minimizing, while Gamma is cost-minimizing only at the switch point.
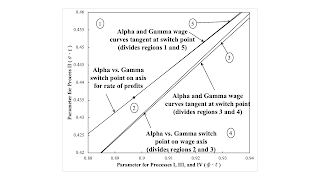
This symmetry extends to partitions of the parameter space, as seen in Figure 2. A locus corresponding to a switch point at which wage curves are tangent bounds a region, 1 or 4, in which no switch points exist. Reswitching occurs in regions 3 and 5, which are on the other side of this boundary. This boundary is tangent to a locus corresponding to the fluke property of a switch point being at the extremes of possible rates of profits, zero or its maximum. The point of tangency in the parameter space corresponds to the double-fluke case under examination.
 |
| Figure 2: Partitions of the Parameter Space around the Second Double-Fluke Case |
| Region | Cost-Minimizing Technique | Notes |
| 1 | Alpha | No switch point. |
| 2 | Alpha, Gamma | Around the switch point, a lower rate of profits is associated with a LESS round-about technique and greater output per worker. |
| 3 | Gamma, Alpha, Gamma | Around the second switch point, a lower rate of profits is associated with a LESS round-about technique and LOWER output per worker. |
| 4 | Gamma | No switch point. |
| 5 | Alpha, Gamma, Alpha | Around the first switch point, a lower rate of profits is associated with a LESS round-about technique. Around the second switch point, a lower rate of profits is associated with LOWER output per worker. |
So far, the partitions in the parameter space have not outlined a region in which triple-switching occurs. Reswitching occurs in regions 3 and 5.