Heterodox
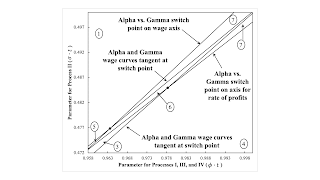
Figure 1: Partitions of the Parameter Space Around the Double-Fluke Switch Points This post is a continuation of this series of posts. The fourth and fifth double-fluke cases, in order of an increasing φ t, are symmetrical. The fourth case has two switch points between Alpha and Gamma. One is on the wage axis. The wage curves are tangent at the other switch point, at a positive rate of profits below the maximum. Alpha is cost-minimizing at all feasible rates of profits. Gamma is cost-minimizing only at the switch points. The fifth case also has two switch points between Alpha and Gamma. One is on the axis for the rate of profits, and the wage curves are tangent at the other switch point. Gamma is cost-minimizing at all feasible rates of profits. Alpha is cost-minimizing only at the
Topics:
Robert Vienneau considers the following as important:
This could be interesting, too:
Asad Zaman writes Newton’s lost revolution: Why his most radical work remains unread
New Economics Foundation writes Are we falling for the myth of minority rule?
Robert Skidelsky writes The American Conservative – Why Is the UK So Invested in the Russia–Ukraine War?
Robert Skidelsky writes The American Conservative: Skidelsky on Russia, Ukraine and the Future of European Security
 |
| Figure 1: Partitions of the Parameter Space Around the Double-Fluke Switch Points |
This post is a continuation of this series of posts.
The fourth and fifth double-fluke cases, in order of an increasing φ t, are symmetrical. The fourth case has two switch points between Alpha and Gamma. One is on the wage axis. The wage curves are tangent at the other switch point, at a positive rate of profits below the maximum. Alpha is cost-minimizing at all feasible rates of profits. Gamma is cost-minimizing only at the switch points. The fifth case also has two switch points between Alpha and Gamma. One is on the axis for the rate of profits, and the wage curves are tangent at the other switch point. Gamma is cost-minimizing at all feasible rates of profits. Alpha is cost-minimizing only at the switch points.
Figure 1 illustrates the partitions of the parameter space around these two double-fluke cases. Region 6, in which triple-switching occurs, extends throughout the figure. A perturbation across a partition corresponding to a switch point at which wages curves are tangent removes two successive switch points along the wage frontier. Thus, two of the switch points in the triple-switching case are lost in region 7, and only one switch point exists for this region.
| Region | Cost-Minimizing Technique | Notes |
| 1 | Alpha | No switch point. |
| 2 | Alpha, Gamma | Around the switch point, a lower rate of profits is associated with a LESS round-about technique and greater output per worker. |
| 3 | Gamma, Alpha, Gamma | Around the second switch point, a lower rate of profits is associated with a LESS round-about technique and LOWER output per worker. |
| 4 | Gamma | No switch point. |
| 5 | Alpha, Gamma, Alpha | Around the first switch point, a lower rate of profits is associated with a LESS round-about technique. Around the second switch point, a lower rate of profits is associated with LOWER output per worker. |
| 6 | Gamma, Alpha, Gamma, Alpha | Around the second switch point, a lower rate of profits is associated with a LESS round-about technique and LOWER output per worker. |
| 7 | Gamma, Alpha | Around the switch point, a lower rate of profits is associated with a more round-about technique and greater output per worker. |