Figure 1: Wage Curves and Rent for an Example of Extensive Rent The analysis of the choice of technique in models of extensive rent can be based on the construction of wage curves, even though the outer envelope does not represent the cost-minimizing technique. The orders of fertility and rentability are emphasized here. The order of fertility is the order in which different qualities of land are introduced into production as requirements for use expand. The order of rentability specifies...
Read More »Fixed Capital And The Emergence Of Reswitching
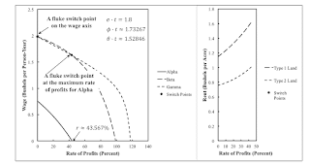
Figure 1: A Wage Frontier With A Fluke Switch Point A fluke example with fixed capital illustrates the emergence of the reswitching of techniques. Table 1 presents coefficients of production in a perturbation of an example from Schefold (1980). With the first process, workers, under the direction of mangers of firms, manufacture new machines. The remaining two processes are used to produce corn. The last process requires an input of an old machine, which is jointly produced with corn by the...
Read More »The Emergence Of The Reverse Substitution Of Labor
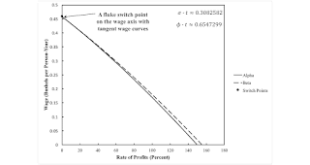
Figure 1: A Wage Frontier With Two Fluke Switch Points This post presents an example with circulating capital alone. Table 1 presents the technology for an economy in which two commodities, iron and corn, are produced. One process is known for producing iron, and two are known for producing corn. Each process is specified by coefficients of production, that is, the required inputs per unit output. The Alpha technique consists of the iron-producing process and the first corn-producing...
Read More »Decades Of Empirical Evidence
I did not always think that mainstream economists are mostly socialized to be unlettered knaves, deficient in mathematics and logic. It took decades of empirical evidence. These links are mostly to tedious and petty stuff, more for my own archiving. Lots of weird stuff comes from non-economists. Sometimes you will find a poster not necessarily defending me, but trying to get some other poster to say something substantial. Some, like Tim Lambert, do not even seem to care about economics....
Read More »My Great-Great-Great-Great-Great-Great-Great-Great-Granduncle Babbitt Murdered a Native-American
The Babbitt family started in America with Edward Bobet, who died in 1675. We have now come to that time of terror and disaster to the settlers the uprising of the Indians, known as King Phillip's War. It can easily be imagined how many anxious hours were passed by Edward and Sarah Bobet, so far removed from the garrison stockade, with their large family of children. Judging by the quantities of Indian relics found on his home farm it would seem that it was a peculiarly favorite haunt of...
Read More »On Sraffian Methodology
I do not know if I will keep on, but I thought I might present a series of posts expanding on this one. By the way, I should have said there that the maximum rate of profits is the reciprocal of the organic composition of capital in Sraffa's standard system, not the actual system. Sraffa's model is descriptive, based on objective data that can be observed for one production period. This data, at least through the first three chapters of The Production of Commodities by Means of...
Read More »George Babbitt’s Neighbor Is A Yale Economist
"On the other side of Babbitt lived Howard Littlefield, Ph.D., in a strictly modern house whereof the lower part was dark red tapestry brick, with a leaded oriel, the upper part of pale stucco like spattered clay, and the roof red-tiled. Littlefield was the Great Scholar of the neighborhood; the authority on everything in the world except babies, cooking, and motors. He was a Bachelor of Arts of Blodgett College, and a Doctor of Philosophy in economics of Yale. He was the...
Read More »Elsewhere
Debate on Marx's theory of value in World Review of Political Economy. Carolina Alves on Joan Robinson on Karl Marx in the Journal of Economic Perspectives. John E. King on Joan Robinson in Jacobin. Jan Toporowski on Michal Kalecki in Jacobin. Maybe to read: Steve Paxton's Unlearning Marx: Why the Soviet Failure was a Triumph for Marx .
Read More »Selective Bibliography For The TSSI
is there a book with a focus exclusively on the TSSI more recent than the 2015 one in this list? Armstrong, Phil (2020). Can Heterodox Economics Make a Difference? Conversations with Key Thinkers Cheltenham: Edward Elgar. Potts, Nick and Andrew Kliman (eds.) (2015). Is Marx's Theory of Profit Right? The Simultaneous-Temporalist Debate. Lanham: Lexington Books. Kliman, Andrew (2007). Reclaiming Marx's "Capital": A Refutation of the Myth of Inconsistency. Lanham: Lexington Books....
Read More »Textbooks for Post-Sraffian Price Theory
This post provides a list of textbooks: Syed Ahmad (1991). Capital in Economic Theory: Neo-classical, Cambridge, and Chaos, Edward Elgar. Christian Bidard (2004). Prices, Reproduction, Scarcity, Cambridge University Press. Duncan K. Foley, Thomas R. Michl, and Daniele Tavani.(2019). Growth and Distribution (2nd edition), Harvard University Press. Richard M. Goodwin (1970). Elementary Economics from the Higher Standpoint, Cambridge University Press. Steve Keen (2011). Debunking...
Read More » Robert Vienneau: Thoughts Economics
Robert Vienneau: Thoughts Economics