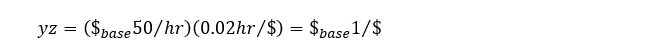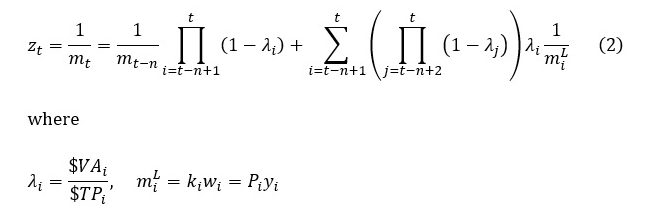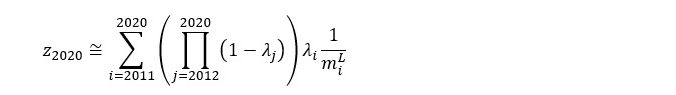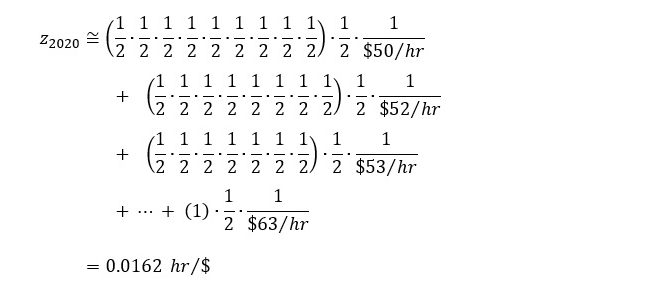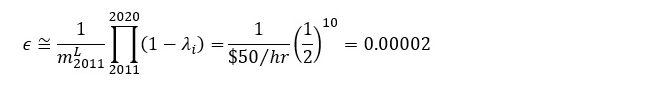The marxian labor-time values of individual commodities fall as productivity improves. This means that if a currency unit is to command a stable quantity of use-values (i.e. physical goods and services) over time, the value of the currency must likewise fall as productivity improves. For a given distribution between wage and profit income, and a given share of value added in total value, a currency unit’s command over use-values will remain stable when money wages rise in line with average productivity. This also promotes price stability. To be clear, for given employment, rising productivity always means that all the currency in existence can purchase more use-values than before. But a single unit of the currency will command more or less use-values according to whether the value of
Topics:
peterc considers the following as important: Economics
This could be interesting, too:
Lars Pålsson Syll writes Schuldenbremse bye bye
Lars Pålsson Syll writes What’s wrong with economics — a primer
Lars Pålsson Syll writes Krigskeynesianismens återkomst
Lars Pålsson Syll writes Finding Eigenvalues and Eigenvectors (student stuff)
The marxian labor-time values of individual commodities fall as productivity improves. This means that if a currency unit is to command a stable quantity of use-values (i.e. physical goods and services) over time, the value of the currency must likewise fall as productivity improves. For a given distribution between wage and profit income, and a given share of value added in total value, a currency unit’s command over use-values will remain stable when money wages rise in line with average productivity. This also promotes price stability.
To be clear, for given employment, rising productivity always means that all the currency in existence can purchase more use-values than before. But a single unit of the currency will command more or less use-values according to whether the value of the currency declines less or more rapidly than commodity values. For a currency unit’s command over use-values to remain stable, the value of the currency must fall at the same rate as productivity improves.
Definition of currency value
In what follows, currency value is defined as the reciprocal of the monetary expression of labor time (MELT). A discussion of this choice and its compatibility with MMT is presented in an earlier post. Background on the MELT, a marxian macro measure enabling conversion between labor time and money, is provided here and here.
In brief, the MELT is the monetary value generated by one hour of socially necessary labor. This makes the reciprocal of the MELT the amount of labor socially necessary to generate a currency-unit’s worth of commodity value. If one hour of socially necessary labor generates $x of monetary value, the MELT is $x per hour and, taking the reciprocal, the value of the currency is 1/x hours per dollar. By this measure, one dollar is worth 1/x hours of socially necessary labor.
The currency’s command over use-values
A currency’s command over use-values depends on the currency’s own value relative to commodity values. Viewed in isolation, the tendency for individual commodity values to fall due to improvements in productivity strengthens a currency’s command over use-values. But the effect can be partially, wholly or more than offset by a fall in the currency’s own value, which primarily reflects growth in money wages and prices.
Let the currency unit be a dollar and, to simplify connections between marxian and non-marxian categories, suppose that all labor is productive.
Average productivity, y, is defined as real output divided by employment. The measure of output is ‘real’ in the sense that, though monetary, it has been deflated by a suitable price index and expressed in terms of base-year dollars. Productivity itself is expressed in base-year dollars of output per unit of employment, or $base/hr. Currency value, z, is expressed in hours of employment per current-year dollar, or hr/$. Therefore, the product yz expresses the amount of base-year dollars commanded by a current-year dollar, or $base/$.
If yz = $basex/$, a dollar currently commands x base-year dollars’ worth of output.
A dollar’s command over use-values (yz) will clearly be linked to the price level P pertaining to final goods and services, which by identity can be written
Here, k is one plus the average pricing markup over money wages (or one plus the nominal rate of surplus value), w is the average money wage and y is average productivity. Depending on the assumptions employed, the link between yz and P can be very simple or slightly more involved.
Simplest case
If productivity is taken as given, the value of the currency depends solely on firms’ average pricing markup and the average money wage:
The product of average productivity and currency value is therefore
In this simple case, the command of a currency unit over real output is measured by the reciprocal of the price level (1/P).
General case
Following the temporal single-system interpretation (TSSI) of Marx’s theory of value, conversions between labor-time and nominal values are complicated by variations in productivity. In a context of ongoing productivity improvements, the appropriate conception of the MELT – and, by implication, of currency value when defined as the MELT’s reciprocal – is the temporal MELT.
The immediate relevance of this is that, with productivity free to vary, currency value depends not only on the average money wage, w, and one plus the markup, k, but also on the share, λ, of monetary value added in total price.
Monetary value added, $VA, is the sum of variable capital, $v, and surplus value, $s, both measured in current dollars. Under the present simplifying assumption that all labor is productive, monetary value added corresponds, in national accounts, to nominal Net Domestic Product (nominal GDP minus Consumption of Fixed Capital).
Total price measured in nominal terms, $TP, is the sum of the nominal advances for constant capital, $c, and variable capital, $v, plus the nominal amount of surplus value $s. In national accounting, $TP is Gross Output, equivalent to the sum of nominal GDP and Intermediate Consumption.
A general formula for the value of the currency is
where TP is total price expressed in hours of socially necessary labor. Starting from this expression, it can be shown that
Currency value at time t is a weighted average of the currency value that applied at time t–1 (z–1) and the currency value that would apply under constant productivity (1/(kw)). The weights reflect the share of monetary value added in total price (λ). This share usually changes only slowly over time.
Multiplying currency value in (1) by average productivity gives
or, recalling that P = kw/y,
In the general case, a dollar’s command over use-values (yz) is still closely related to the reciprocal of the price level, which pertains to final goods and services, but now also depends on factors relating to intermediate goods and services (reflected in λ and the currency value that applied when these goods and services entered production).
A conceptual simplification is to define ‘total productivity’, yT, as ‘real total price’ divided by ‘total labor time’. Real total price, T, is nominal total price deflated by an index, PT, of the prices applying to both final and intermedite goods and services. Total labor, LT, is the sum of labor transferred from inputs (‘dead labor’) and labor performed during the current period (‘living labor’). The value of the currency is then
Multiplying through by average productivity,
In this way, a currency unit’s command over use-values can still be regarded as the reciprocal of a suitable price index. It is just that the price index needs to reflect the prices of intermediate goods and services in addition to the prices of final goods and services.
An Implication
In the context of gradual, ongoing improvements in productivity, it is desirable to manage a gradual, ongoing decline in the value of the currency. The best way to do this is to encourage or legislate money wage growth in line with average productivity or otherwise foster the institutions and economic conditions conducive to such a development. To hold currency value constant while productivity improves would be deflationary, making private debt obligations more burdensome in real terms.
As already indicated, a falling currency value does not necessarily imply a weakening of the currency’s command over real output. A dollar’s command over real output (yz) only weakens if currency value falls faster than average productivity improves.
To illustrate, if average productivity is 50 base-year dollars of output per hour of employment and currency value is 0.02 hours of employment per dollar,
and a current-year dollar commands a base-year dollar’s worth of output.
If productivity doubles and currency value halves, a dollar’s command over use-values stays the same:
As before, a dollar commands a base-year dollar’s worth of output.
In general, a dollar’s command over use-values remains unchanged when productivity grows at the same rate as currency value shrinks. Or, bearing in mind that the MELT is the reciprocal of currency value, a dollar’s command over use-values is stable when productivity and the MELT grow at the same rate.
Estimating currency value when the start-of-period currency value is unknown
Currency value at time t can be calculated using expression (1) when the currency value of time t–1 is known. But if an earlier currency value is unknown, it is necessary to estimate an initial currency value.
Since currency value, as defined here, is simply the reciprocal of the MELT, the task of finding an initial currency value is the same as finding an initial MELT. An earlier post outlined a method of estimating the MELT when no earlier MELT is known. The same procedure leads to the following formula for estimating currency value when no earlier currency value is known:
The first part of the right-hand side of (2) approaches zero as n gets large. This means that currency value can be approximated to a desired degree of accuracy (through choice of n) using the formula
In (2) and (3), zt is currency value at time t, mt is the MELT of time t, n is the number of periods we choose to look back in obtaining an estimate of currency value (the further we look back, the more accurate the estimate), i and j are indices used in the summation, λ is the share of monetary value added in total price, and mL is the ‘monetary expression of living labor’ or MELL (equal to monetary value added divided by employment, $VA/L, or equivalently, one plus the markup multiplied by the average money wage, kw, or again equivalently, the average price level applying to final goods and services multiplied by average productivity, Py). The estimate of currency value provided by (3) is therefore a weighted average of the reciprocals of earlier MELLs and primarily reflects past – especially the most recent – behavior of prices and productivity. The weights (which are the products of λ’s and 1–λ’s) approach zero as n becomes large (the further we look back), because λ always takes a value between zero and one.
To illustrate, suppose that we look back ten periods (n=10) from the vantage point of period t=2020. Applying (3),
Suppose that the share of monetary value added in total price has been a stable fifty percent over the ten periods (all the lambdas are 0.5) and that the MELLs (equal to net domestic product divided by employment) from earliest to latest happened to be $50/hr, $52/hr, $53/hr, $55/hr, $56/hr, $57/hr, $59/hr, $60/hr, $62/hr and $63/hr. Substituting these numbers,
The first term in (2) can be used to get an idea of the likely magnitude of the error, ϵ, in this approximation:
The MELT of n periods ago, m2011, is unknown but likely to be similar to the MELL of the same year (somewhat less than the MELL if prices rose over 2011). The error in approximating the value of the currency in 2020 will be in the vicinity of
which is about 0.12 percent of the approximated currency value. If greater precision is desired, it is necessary to look back further in time (set a larger n).