The Rate of Profits is Not the Scale Factor

by
Robert Vienneau
My articles My siteMy booksMy videos
Follow on:

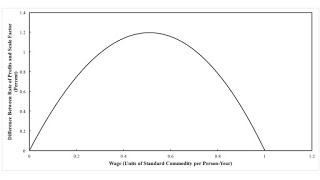
Figure 1: Rate of Profits Unequal to Scale Factor for Rate of Profits

This post continues the example in the previous post. I modify the prices equations so that the rate of profits in producing corn is (s₁ r̂), and the rate of profits in producing ale is (s₂ r̂). The solution to the price equations are:

p_corn = 16 [16 + (s₁ - s₂) r̂]/[204 + (3 s₁ + 9 s₂) r̂]

p_ale = 32 [10 - (s₁ - 3 s₂) r̂]/[204 + (3 s₁ + 9 s₂) r̂]

w = 4 [51 - (9 s₁ + 5 s₂) r̂ - s₁s₂ r̂²]/[204 + (3 s₁ + 9 s₂) r̂]

where r̂ is what I have been calling the scale factor for the rate of profits.

I want to show that, only in exceptional cases can the the markups s₁ and s₂ be rescaled such that the scale factor is equal to the economy-wide rate of profits, whatever the distribution of income. For concreteness, assume that the rate of profits is four times as high in the corn industry, as compared to the ale industry. That is, introduce a new parameter α such that:

s₁ = α

s₂ = (1/4) α

Suppose the wage is unity and workers receive the entire standard commodity. Then both the scale factor for the rate of profits and the rate of profits are identically zero percent.

Next, consider the other extreme case, where the wage is zero. The maximum rate of profits is 300 percent. For the scale factor to also be three, the numerator for the wage, in the third equation above must be zero, when a rate of profits of 300 percent and the above scale factors are substituted in. One thereby obtains a quadratic equation:

3 α² + 41 α - 68 = 0

The positive solution is:

α = (1/6)( -41 + 2,497^1/2)

For any scale factor for the rate of profits, one can find the wage with these markups. For any wage, one can find the economy-wide rate of profits:

r = 3 (1 - w)

The simplicity of the above equation results from taking the standard commodity as the numeraire. The graph at the top of this post shows the difference between the rate of profits and the scale factor, as a function of the proportion of the standard commodity paid out in wages. The rate of profits and the scale factor are equal only at the two extremes. I guess that in a model with more commodities, the difference does not come out looking like a quadratic function.

This counterexample demonstrates that, in general, one cannot rescale markups such that the scale factor for the rate of profits is the economy-wide rate of profits, however distribution stands. Part of Marx's point in Capital is that observers who focus on surface phenomena will not perceive underlying value relations.

"The relations connecting the labour of one individual with that of the rest appear, not as direct social relations between individuals at work, but as what they really are, material relations between persons and social relations between things."

I guess I have shown that the existence of persistent ratios between the rate of profits in various industries, as with a corporate sector and a sector of small firms and proprietorships, provides another layer of confusion in economic analysis. Here is a source of another illusion created by competition.

Aside: I have stumbled across the International Symposium on Marxian Theory (ISMT). They have a series of books out, with a focus on reacting to the complete works of Marx and Engels (MEGA²). MEGA² is published under the auspices of the Internationale Marx-Engels-Stiftung (IMES) in Amsterdam and of other groups in other countries. Apparently, volume 1 of Capital varied among editions, and Marx had several drafts. Furthermore, MEGA² apparently has editions of volumes 2 and 3 that show exactly how Engels edited them. These facts re-enforce the point of this post, not that I want to read all of these variants.