Heterodox
Figure 1: Wage-Rate of Profits Curves Consider a comparison of comparison of stationary states. Net output is taken as given, and a unit of net output is the numeraire. Technology consists of a finite set of techniques. In each technique, net output is produced from inputs of labor and produced circulating capital goods. No fixed capital is used, and land of the best quality is in such abundance that it is free. Also assume constant returns to scale. One can find a wage-rate of profits curve for each technique. The cost-minimizing technique at is the technique its wage curve on the outer envelope, also known as the wage-rate of profits frontier, at that wage. Switch points are points at which two or more wage curves intersect (on the frontier). Suppose the same gross vector
Topics:
Robert Vienneau considers the following as important: Example in Mathematical Economics, Labor Markets, Sraffa Effects
This could be interesting, too:
Robert Vienneau writes The Production Of Commodities And The Structure Of Production: An Example
Robert Vienneau writes A Derivation Of Prices Of Production With Linear Programming
Robert Vienneau writes Reswitching Pattern In Corn-Tractor Model
Robert Vienneau writes Goal: Perturb Special Case Of Steedman’s Corn-Tractor Model
|
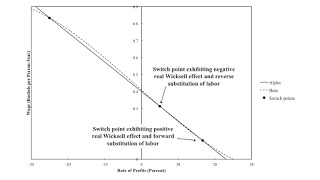
| Figure 1: Wage-Rate of Profits Curves |
Consider a comparison of comparison of stationary states. Net output is taken as given, and a unit of net output is the numeraire. Technology consists of a finite set of techniques. In each technique, net output is produced from inputs of labor and produced circulating capital goods. No fixed capital is used, and land of the best quality is in such abundance that it is free. Also assume constant returns to scale.
One can find a wage-rate of profits curve for each technique. The cost-minimizing technique at is the technique its wage curve on the outer envelope, also known as the wage-rate of profits frontier, at that wage. Switch points are points at which two or more wage curves intersect (on the frontier). Suppose the same gross vector commodities are produced, albeit in different proportions, at a switch point. Generically, the techniques differ in the process in use for one industry. The same processes are in use in all other industries. (I have argued that fluke switch points in which wage curves for more than two techniques intersect at a single switch point are of importance for understanding how qualitative changes in the properties of the wage frontier can come about from, for example, technological progress.)
A generic switch point can exhibit positive or negative real Wicksell effects. And it can exhibit a forward or reverse substitution of labor.
Around a switch point with a positive real Wicksell effect, a higher wage is associated with firms wanting to employ more labor throughout the economy, per unit of net output.
Around a switch point with a reverse substitution of labor, a higher wage is associated with firms, in the industry in which the process of production varies, wanting to employ more labor per unit of gross output.
I have previously given a numerical example that illustrates switch points with:
- A positive real Wicksell effect and a reverse substitution of labor.
- A negative real Wicksell effect and a reverse substitution of labor.
- A negative real Wicksell effect and a forward substitution of labor.
Figure 1 illustrates a switch point can have a positive real Wicksell effect and a forward substitution of labor. Suppose that the wage curves for two techniques have three intersections. One intersection is between a rate of profits of negative one hundred percent and zero. The other intersections are at two feasible poisitive rates of profits. Then the switch point at the largest positive rate of profits has a positive real Wicksell effect and a forward substitution of labor. (I have not actually specified a technology, with three or more produced commodities, that generates wage curves like those illustrated.)
Since all four possible combinations are possible, the direction of real Wicksell effects and the substitution of labor are independent of of one another. The choice of technique results in variation in gross outputs in multiple industries, for given net outputs. These variations also result in variation in the amount of labor firms want to employ. This variation in aggregate employment is consistent with any direction in the variation in the labor coefficient of production in the industry with the varying process.
If somebody explains wages and employment by supply and demand for labor, they are making a political point. This holds even if they argue that a supply and demand explanation provides a baseline. They may be demonstrating that economists continue to adopt a price theory that has been known for decades to be incoherent nonsense.