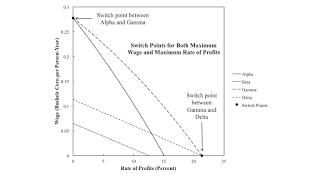
Figure 1: Wage Frontier for a Fixed Capital Example1.0 Introduction I continue to explore the simplest multisector model of the production of commodities by means of commodities in which circulating and fixed capital is used in both sectors. In previous explorations, I locate a four-technique pattern, observe recurrence of truncation, and provide an example in which truncating all machines is infeasible. I think my taxonomy of fluke switch points and methods of visualizing the effects of perturbing parameters, such as coefficients of production, applies unchanged to models of the production of commodities with fixed capital, maybe with certain simplifying assumptions. So I want to, at least, show fluke swith points of co-dimension one in models of fixed capital. Every switch point is
Topics:
Robert Vienneau considers the following as important: Austrian School Of Economics, Example in Mathematical Economics, Joint Production
This could be interesting, too:
Robert Vienneau writes Austrian Capital Theory And Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes Double Fluke Cases For Triple-Switching In The Corn-Tractor Model
Robert Vienneau writes The Emergence of Triple Switching and the Rarity of Reswitching Explained
Robert Vienneau writes Recap For A Triple -Switching Example
| Figure 1: Wage Frontier for a Fixed Capital Example |
I continue to explore the simplest multisector model of the production of commodities by means of commodities in which circulating and fixed capital is used in both sectors. In previous explorations, I locate a four-technique pattern, observe recurrence of truncation, and provide an example in which truncating all machines is infeasible.
I think my taxonomy of fluke switch points and methods of visualizing the effects of perturbing parameters, such as coefficients of production, applies unchanged to models of the production of commodities with fixed capital, maybe with certain simplifying assumptions. So I want to, at least, show fluke swith points of co-dimension one in models of fixed capital.
Every switch point is specified by the condition that two techniques be cost-minimizing at that switch point. The co-dimension is the number of additional conditions that must be met by that switch point:
- A pattern over the wage axis: The rate of profits is zero at the switch point.
- A pattern over the axis for the rate of profits: The wage is zero at the switch point.
- A three-technique pattern: A third technique is cost-minimizing at the switch point.
- A reswitching pattern: The two wage curves at the switch point.
So I am thinking of how to bring my examples of fixed capital together to show that all of these flukes are available with fixed capital. This post presents a global pattern which combines a pattern over the wage axis and a pattern over the axis for the rate of profits.
2.0 TechnologyTable 1 specifies the coefficients of production for the example. In both the machine sector and the corn sector, an old machine cannot be transferred to the other sector. Corn is the consumption good and also acts as circulating capital. This is the simplest mutli-sectoral structure with both circulating and fixed capital in all sectors. The available techniques are defined in Table 2, unchanged from previous posts.
| Input | Process | |||
| (I) | (II) | (III) | (IV) | |
| Labor | 1/10 | 8 | 43/40 | 1 |
| Corn | 0.548800712 | 1.7443584 | 0.125 | 0.282386 |
| New Machines | 1 | 0 | 1 | 0 |
| Old Machines A | 0 | 1 | 0 | 0 |
| Old Machines B | 0 | 0 | 0 | 1 |
| Outputs | ||||
| Corn | 0 | 0 | 1 | 0.56 |
| New Machines | 2 | 5/2 | 0 | 0 |
| Old Machines A | 1 | 0 | 0 | 0 |
| Old Machines B | 0 | 0 | 1 | 0 |
| Technique | Processes |
| Alpha | I, III |
| Beta | I, II, III |
| Gamma | I, III, IV |
| Delta | I, II, III, IV |
The choice of technique can be analyzed by the construction of the wage frontier. Corn is the numeraire, and wages are assumed to be paid out of the surplus at the end of the year. As shown in Figure 1 above, the Gamma technique is cost-minimizing at any possible distribution of income. The economic life of a machine is truncated in the machine sector and operated for the full two years in the corn sector. At a rate of profits of zero, it is also cost-minimizing to truncate the machine in the corn sector. At a maximum rate of profits, it is also cost-minimizing to operate the machine for the full two years in the machine sector.
The analysis of the choice of technique is re-inforced by looking at prices. Figure 2 plots the price of a new machine as a function of the rate of profits, for all four techniques. At a switch point, the price of a new machine is the same for both techniques cost-minimizing at that rate of profits.
| Figure 2: Price of New Machine |
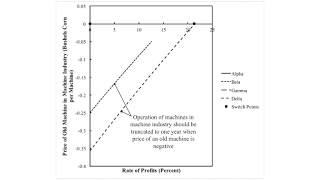
Figure 3 plots the price of an old machine in the machine sector. This price is zero for the Alpha and Gamma techniques, in which the economic life of the machine in the machine sector is truncated to one year. Up to the maximum rate of profits, the price of this type of old machine is negative for the Beta and Delta techniques. Thus, these techniques are not cost-minimizing. If either one of these techniques was in operation, managers of firms would be incentivized to truncate the operation of the machine after one year in the machine sector. At the switch point at the maximum rate of profits, the price of the old machine is zero. Thus, the machine could be operated for two years in the machine sector when the workers live on air.
| Figure 3: Price of Old Machines in Machine Sector |
Figure 4 shows the price of an old machine in the corn sector. Here the price of an old machine is zero for the Alpha and Beta techniques. The switch points are shown.
| Figure 4: Price of Old Machines in Corn Sector |
I now look at a slice of parameter space around the fluke case above. Consider small variations in a1,1 and a1,2, the bushels of corn need for input for a unit level of operation of the processes in the machine sector. At a unit level, these processes operate with a new machine and a one-year old machine, respectively, to produce new machines for use in either sector.
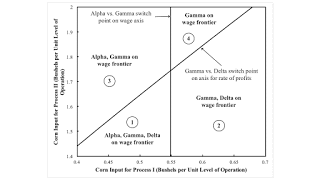
Figure 5 shows this slice of the parameter space around the fluke switch points in Figure 1. Variation in a1,2 has no effect on the wage curves for the Alpha and Gamma techniques. Hence, the pattern over the wage axis is a vertical line in the figure. The pattern over the axis for the rate of profits is a diagonal line. The figure shows which techniques are cost-minimizing in which of the four 'quadrants' in which I have partitioned the parameter space.
| Figure 5: Selected Regions in Parameter Space |
Tables 3 and 4 summarize this local analysis. Around all switch points in illustrated regions of the parameter space, a lower rate of profits is associated with greater net output per person-year. In some sense, a lower rate of profits is associated, in this example, with the adoption of a more capital-intensive technique. But, for all switch points, examined here this increase in the amount of 'capital' used per worker is associated with a decrease in the economic life of a machine, in one sector or the other.
| 1 | 0 ≤ r ≤ r1 | Operation of machine truncated in both sectors. |
| r1 ≤ r ≤ r2 | Operation of machine truncated after 1 year in machine sector. Operated for 2 years in corn sector. | |
| r1 ≤ r ≤ rδ | Machine operated for 2 years in both sectors. | |
| 2 | 0 ≤ r ≤ r1 | Operation of machine truncated after 1 year in machine sector. Operated for 2 years in corn sector. |
| r1 ≤ r ≤ rδ | Machine operated for 2 years in both sectors. | |
| 3 | 0 ≤ r ≤ r1 | Operation of machine truncated in both sectors. |
| r1 ≤ r ≤ rγ | Operation of machine truncated after 1 year in machine sector. Machine operated for 2 years in corn sector. | |
| 4 | 0 ≤ r ≤ rγ | Operation of machine truncated after 1 year in machine sector. Machine operated for 2 years in corn sector. |
| 1 | Larger rate of profits associated with longer economic life of machine in both sectors. |
| 2 | Larger rate of profits associated with longer economic life of machine in machine sector. |
| 3 | Larger rate of profits associated with longer economic life of machine in corn sector. |
| 4 | No switch points. |
So that is another example of patterns around the wage axis and the axis for the rate of profits. I still have not found in this particular model examples of reswitching or capital-reversing. But I have such examples in other models of fixed capital. The above example, however, re-iterates that no connection exists between lengthening the economic life of a machine and an increase in the supply of 'capital'. Bohm-Bawerk was not incorrect merely because of the difficulty of defining a measure of the average period of production. His intuition, and not just his, on how prices work was itself incorrect.
 Heterodox
Heterodox