Heterodox
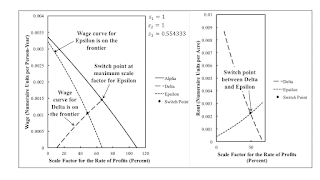
Figure 1: Wage Curves and Rent for an Example of Intensive Rent This post is a continuation of a previous example. This is a fluke case insofar as the Alpha and Delta wage curves intersect at the scale factor for the rate of profits that is the maximum possible for the Epsilon technique. This fluke case is associated with a qualitative change in the range of the scale factor for the rate of profits in which no cost-minimizing technique exists. The technology, endowments, requirements for use, and techniques are as previously defined. Requirements for use can only be satisfied by the Alpha, Delta, and Epsilon techniques. I continue to consider markup pricing. The rate of profits is (s1r), (s2r), and (s3r) in the iron, steel, and corn industries. In determining which technique is
Topics:
Robert Vienneau considers the following as important: Full Cost Prices, rent, Sraffa Effects
This could be interesting, too:
Robert Vienneau writes A 1-Dimensional Diagram For Extensive Rent With Markup Pricing
Robert Vienneau writes Extensive Rent With Markup Pricing: An Example
Robert Vienneau writes Reswitching Pattern In Corn-Tractor Model
Robert Vienneau writes Wages, Employment Not Determined By Supply And Demand
 |
| Figure 1: Wage Curves and Rent for an Example of Intensive Rent |
This post is a continuation of a previous example.
This is a fluke case insofar as the Alpha and Delta wage curves intersect at the scale factor for the rate of profits that is the maximum possible for the Epsilon technique. This fluke case is associated with a qualitative change in the range of the scale factor for the rate of profits in which no cost-minimizing technique exists.
The technology, endowments, requirements for use, and techniques are as previously defined. Requirements for use can only be satisfied by the Alpha, Delta, and Epsilon techniques.
I continue to consider markup pricing. The rate of profits is (s1r), (s2r), and (s3r) in the iron, steel, and corn industries. In determining which technique is cost-minimizing, r, the scale factor for the rate of profits is taken as given.
Figure 1, at the top of this post, depicts the wage and rent curves for the different techniques. The wage curves for the cost-minimizing techniques lie on the wage frontier. The wage frontier consists of the wage curves for the Delta and Epsilon techniques up to the switch point between them. The wage frontier ends there. No technique is cost-minimizing between this switch point and the maximum scale factor for the rate of profits for Alpha.
Table 1 goes into more detail on the wage curves than aqnybody probably cares about. I introduce some notation that I will find useful in later posts. Rδ is the scale factor for the rate of profits at which the wage is zero for Delta. R*,δ is the scale factor for the rate of profits at which the rent is zero for Delta. This is a fluke case because R*,δ is equal to Rε. Anyways, in the first range for the scale factor, only the Alpha and Epsilon techniques have wage curves that are eligible to lie on the wage frontier; the wage curve for the Delta technique lies below the axis for the scale factor for the rate of profits. In the next two ranges, all three wage curves are eligible. In the last range of the scale factor, only the wage curve for Alpha is eligible. The rent curve for Delta and the wage curve for Epsilon lie below the axis for the scale factor.
| Lower Bound on r | Upper Bound on r | Techniques |
| 0 percent | Rδ | Alpha has a positive wage |
| Delta has a negative wage | ||
| Epsilon has a positive wage and positive rent | ||
| Epsilon is uniquely cost-minimizing | ||
| Rδ | r* | Alpha has a positive wage |
| Delta has a positive wage and positive rent | ||
| Epsilon has a positive wage and positive rent | ||
| Delta is non-uniquely cost-minimizing | ||
| Epsilon is non-uniquely cost-minimizing | ||
| r* | R*,δ | Alpha has a positive wage |
| Delta has a positive wage and positive rent | ||
| Epsilon has a positive wage and positive rent | ||
| No cost-minimizing technique exists | ||
| R*,δ | Rα | Alpha has a positive wage |
| Delta has a positive wage and negative rent | ||
| Epsilon has a negative wage and positive rent | ||
| No cost-minimizing technique exists |
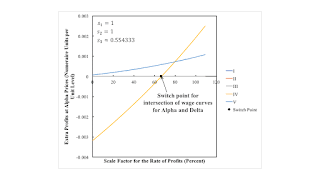
I plot extra profits for each process for each technique to demonstrate my claims about which technique is cost-minimizing. Figure 2 shows extra profits for each process at Alpha prices. Extra profits are zero for the three processes comprising the technique. The last corn-producing process can always pay extra profits for any scale factor, while the penultimate process can pay extra profits for any scale factor greater than that at the intersection of the Alpha and Delta wage curves and not exceeding the maximum scale factor for the Alpha technique. The Alpha technique is never cost-minimizing.
 |
| Figure 2: Extra Profits with Alpha Prices |
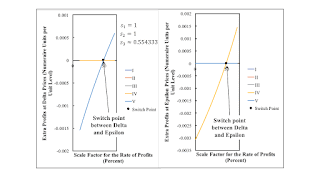
Figure 3 plots extra profits for each process for the Delta and Epsilon techniques. Since four of the five processes in the technology are operated for each technique, four of the five processes obtain extra profits of zero for all scale factors between the limits for each technique. If the Delta technique were in operation at a scale factor greater than at the switch point between Delta and Epsilon, farmers would start to operate the fifth process, moving away from the Delta technique. If the Epsilon technique were in operation in this range, farmers would start to operate the fourth technique. A market algorithm would not coverge to any technique for a scale factor for the rate of profits greater than that at the switch point between Delta and Epsilon and not exceeding the maximum scale factor for the Alpha technique.
 |
| Figure 3: Extra Profits with Delta or Epsilon Prices |
For a smaller markup in agriculture than in this fluke case, three interesting ranges of the scale factor exist where no technique is cost-minimizing. In the first, the Alpha, Delta, and Epsilon techniques can all pay positive wages and non-negative rents, with positive prices. In the second, only the Alpha and Delta techniques can pay positive wages and a non-negative rent. In the third, the Alpha technique can pay a positive wage, while the Delta technique cannot pay a positive rent.
For a larger markup than in the fluke case, the second interesting range of the scale factor has changed. The Delta technique can no longer pay a positive rent. Instead, the Alpha and Epsilon techniques can pay positive wages and non-negative rents, with positive prices.