Figure 1: Wage Curves for the Two Techniques1.0 Introduction Economists following the Austrian school often represent the structure of production with Hayekian triangles (Hayek 1931, Rothbard 1962, Skousen 1990, Garrison 2001, Machaj 2017). Typically, goods of the highest order are produced with unaided labor or other unproduced original resources. (Fillieule (2007), in which a Hayekian triangle is constructed with an infinite stream of unproduced inputs, is an exception.) Rarely, is a...
Read More »A Derivation Of Prices Of Production With Linear Programming
1.0 Introduction This post illustrates a derivation of prices of production, based on certain properties of duality theory as applied to linear programming. I strive to be more concise and elementary than previous expositions. This exposition is based on John Roemer's Reproducible Solution (Analytical Foundations of Marxian Economic Theory, Cambridge University Press, 1981). You will find no utility maximization or supply and demand functions below. I have no need for such hypotheses....
Read More »Reswitching Pattern In Corn-Tractor Model
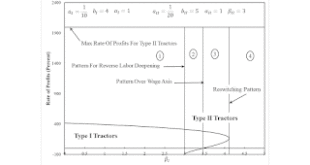
Figure 1: Variation in the Cost-Minimizing Technique with Selected Coefficient of Production This post reports on some work with Steedman's corn-tractor model. I have yet to find an instance of triple-switching. I have found a case of reswitching, though. Figure 1 above and Table 1 below show how switch points vary with perturbations of the labor needed to produce a bushel of corn in the corn industry with Type I tractors. Only one switch point exists in region 1. Around this switch point...
Read More »Goal: Perturb Special Case Of Steedman’s Corn-Tractor Model
1.0 Introduction I would like to illustrate triple switching, in the corn-tractor model, with one of my one-dimensional diagrams. I have a triple-switching example, from Bertram Schefold, but the wage-rate of profit frontier is not visually striking in it. Such an example would not be worthy of a research paper. But perhaps I could modify a section of my recent working paper to submit somewhere. Besides, posing a new problem might motivate me to update my computing technology. 2.0...
Read More »Von Mises Wrong On Economic Calculation
1.0 Introduction I have explained this before. Suppose one insists socialism requires central planning. In his 1920 paper, 'Economic calculation in the socialist commonwealth', Ludwig Von Mises claims that a central planner requires prices for capital goods and unproduced resources to successfully plan an economy. The claim that central planning is impossible without market prices is supposed to be a matter of scientific principle. Von Mises was mistaken. His error can be demonstrated to...
Read More »Wages, Employment Not Determined By Supply And Demand
1.0 Introduction I do not think I have presented an introductory example in a while in which an increased wage is associated with firms wanting to employ more labor, given the level of net output. This example is presented as a matter of accounting for a vertically integrated firm. Exact calculations with rational numbers are tedious in this example. I expect that if anybody bothers to check this, they would use a spreadsheet. As far as I can tell, Microsoft Excel uses double precision...
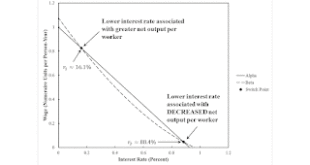
Read More »A Perverse Switch Point For Neoclassical Economics, Non-Perverse For Austrians
Figure 1: The Wage-Rate of Profits Frontier1.0 Introduction This post completes a demonstration that the economic life of a machine is independent of the capital-intensity of a technique. I here fill in the upper right of a two-by-two table. I have previously filled in the upper-left and lower right entries. And I also have an example for the lower left. 2.0 Technology Tables 1 and 2 present coefficients of production for processes which can be combined to produce a new output of corn....
Read More »The Fundamental Sraffian Theorem
1.0 Introduction I have been reading Robin Hahnel. Hahnel argues even more strongly than Steedman did that labor values are redundant. And he argues for the importance of the fundamental Sraffian theorem. I think this may be Hahnel's coinage. Anyways' this is my working my way through some of what I think he is saying. Hahnel has some interesting things to say, not discussed here, about analyzing environmental concerns in a Sraffian framework. I ignore the chapter in Hahnel (2017) on the...
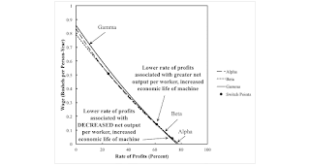
Read More »Perverse Switch Point For Austrian Economics
Figure 1: The Wage-Rate of Profits Frontier This post continues a series of posts demonstrating that the change in the economic life of a machine at a switch point is independent of the change of the capital intensity of the technique at a switch point. I here fill in the lower left in a a two-by-two table. The wage curves above are for the an example with the same structure as in the previous post in this series.This is a 'one-good' model. The manager of firms know three processes to...
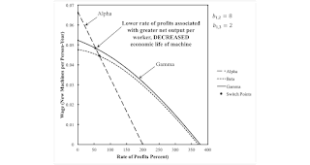
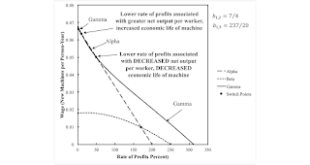
Read More »Traditional And ‘Perverse’ Switch Points For Austrian And Neoclassical Economics
Figure 1: The Wage-Rate of Profits Frontier1.0 Introduction This is one in a series of posts demonstrating that the change in the economic life of a machine at a switch point is independent of the change of the capital intensity of the technique at a switch point. I want to illustrate each entry in a two-by-two table in a previous post. The example in this post has two switch points. One fits the traditional Austrian and neoclassical stories, as in the entry in the upper-left of the table....
Read More » Heterodox
Heterodox