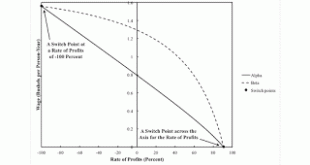
Figure 1: Switch Points On The Axis For The Rate Of Profits And At r = -100 Percent This is an example of a fluke case in the analysis of the choice of technique. The interest in flukes, for me, is that they show how the characteristics of markets can change. They provide insight into structural economic dynamics, as Luigi Pasinetti calls it. I have previously shown a fluke case, with a switch point on the axis for the rate of profits with a real Wicksell effect of zero. A perturbation...
Read More »A Market Algorithm
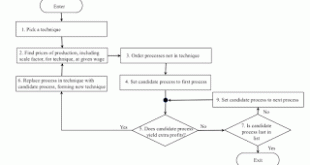
Figure 1: Specification of a Market Algorithm1.0 Introduction This article is heavily based on Bidard (2004). An approach to the analysis of the choice of technique, in keeping with construction of the outer envelope of wage curves, is to consider replacing processes, more or less, one at a time. This post presents this approach as following an algorithm. Assume that a set of techniques exist where all techniques are at least viable, indecomposable, and produce the same set of...
Read More »Another Example Of The Factor Price Frontier In The Space Of Rental Prices
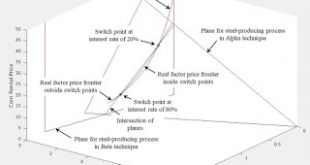
Figure 1: Real Factor Price Frontier1.0 Introduction I am planning on posting at an even slower rate for a while. This post continues my exploration of a way of visualizing the choice of technique proposed by Carlo Milana. In this post, I show how to correctly apply his visualization to an example from my 2017 ROPE paper. 2.0 Technology Two techniques are available for producing corn, the consumption good. Each technique consists of a flow-input, point-output technology, with a finite...
Read More »Update To Example In Vienneau (2019)
Maybe this post should be titled "Erratum" or "corrigendum". I have an example in my paper last year in which wage frontiers are supposed to vary with two parameters. One is the markup in the "iron" industry. And the other is σ t. The example should be as in Table 1. All the theory and the visualizations in the paper work out with this example. Table 1: Technology for Producing Steel and Corn InputIndustryIronCornAlphaBetaLabora0,1 = 1aα,0,2(t) = (5191/5770) e(1/10) - σ taβ,0,2 =...
Read More »Reswitching With Markup Pricing And Fixed Capital
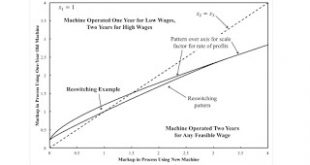
Figure 1: Two Dimensional Pattern Diagram1.0 Introduction This post extends an example from Bertram Schefold. It presents markup pricing in an example with a machine that can be operated for two years or junked after one year. This is a case of joint production in which, unlike in some cases, the choice of technique can still be analyzed by the construction of the wage frontier. Also, I do not think the question of requirements for use enter in here, and all matrices are square. As usual,...
Read More »Towards the Derivation of the Cambridge Equation with Expanded Reproduction and Markup Pricing
I have a new working paper. Abstract: Does the Cambridge equation, in which the rate of profits in a steady state is equal to the quotient of the rate of growth and the savings rate out of profits, hold in an economy with widespread non-competitive markets? This article presents a multiple-good model of markup pricing in an attempt to answer this question. A balance equation is derived. Given competitive conditions, this model can be used to derive the Cambridge equation. The Cambridge...
Read More »The Factor Price Frontier In The Space Of Factor Rental Prices
Figure 1: Real Factor Price Frontier1.0 Introduction Carlo Milana has proposed a new way of visualizing the choice of technique, including in the case of reswitching. This way of describing what he has done is not neccessarily how he thinks of it. In this post, I describe his approach with a reswitching example, in a model of the production of commodities by means of commodities. 2.0 Technology Table 1 shows the coefficients of production for this example. Coefficients of production...
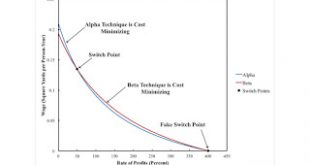
Read More »A Fake Switch Point in an Example With Circulating Capital
Figure 1: A Switch Point and a Fake Switch Point on Wage Curves1.0 Introduction In the analysis of the choice of technique, I typically consider examples of technology with a finite number of techniques. For each technique, I find the wage as a function of the rate of profits. The outer envelope of these curves shows the cost-minimizing technique at each rate of profits (or each level of the wage). Points on more than one wage curve are switch points. This approach is valid when, for...
Read More »The Cambridge Equation, Expanded Reproduction, and Markup Pricing: An Example
1.0 Introduction I have sometimes set out Marx's model of expanded reproduction, only with prices of production instead of labor values. I assume two goods, a capital good and a consumption good, are produced with constant technology. If one assumes workers spend all their wages and capitalists save a constant proportion of profits, one can derive the Cambridge equation in this model. The Cambridge equation shows that, along a steady state growth path, the economy-wide rate of profits is...
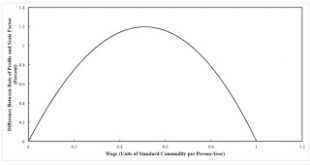
Read More »The Rate of Profits is Not the Scale Factor
Figure 1: Rate of Profits Unequal to Scale Factor for Rate of Profits This post continues the example in the previous post. I modify the prices equations so that the rate of profits in producing corn is (s1 r̂), and the rate of profits in producing ale is (s2 r̂). The solution to the price equations are: pcorn = 16 [16 + (s1 - s2) r̂]/[204 + (3 s1 + 9 s2) r̂] pale = 32 [10 - (s1 - 3 s2) r̂]/[204 + (3 s1 + 9 s2) r̂] w = 4 [51 - (9 s1 + 5 s2) r̂ - s1s2 r̂2]/[204 + (3 s1 + 9 s2) r̂]...
Read More » Heterodox
Heterodox