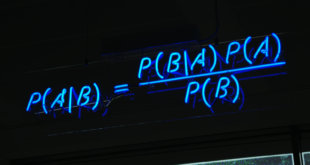Tag Archives: Theory of Science & Methodology

.[embedded content]

The Holy Grail of Science Traditionally, philosophers have focused mostly on the logical template of inference. The paradigm-case has been deductive inference, which is topic-neutral and context-insensitive. The study of deductive rules has engendered the search for the Holy Grail: syntactic and topic-neutral accounts of all prima facie reasonable inferential rules. The search has hoped to find rules that are transparent and algorithmic, and whose following...

Statistical philosophies and idealizations As has been long and widely emphasized in various terms … frequentism and Bayesianism are incomplete both as learning theories and as philosophies of statistics, in the pragmatic sense that each alone are insufficient for all sound applications. Notably, causal justifications are the foundation for classical frequentism, which demands that all model constraints be deduced from real mechanical constraints on the...

The bias toward the superficial and the response to extraneous influences on research are both examples of real harm done in contemporary social science by a roughly Bayesian paradigm of statistical inference as the epitome of empirical argument. For instance the dominant attitude toward the sources of black-white differential in United States unemployment rates (routinely the rates are in a two to one ratio) is “phenomenological.” The employment differences are traced to...

Scientific realism and inference to the best explanation In inference to the best explanation we start with a body of (purported) data/facts/evidence and search for explanations that can account for these data/facts/evidence. Having the best explanation means that you, given the context-dependent background assumptions, have a satisfactory explanation that can explain the fact/evidence better than any other competing explanation — and so it is reasonable to...

Why Bayesianism doesn’t resolve scientific disputes The occurrence of unknown prior probabilities, that must be stipulated arbitrarily, does not worry the Bayesian anymore than God’s inscrutable designs worry the theologian. Thus Lindley (1976), one of the leaders of the Bayesian school, holds that this difficulty has been ‘grossly exaggerated’. And he adds: ‘I am often asked if the [Bayesian] method gives the right answer: or, more particularly, how do you...

Although Bayes’ theorem is mathematically unquestionable, that doesn’t qualify it as indisputably applicable to scientific questions. Science is not reducible to betting, and scientific inference is not a branch of probability theory. It always transcends mathematics. The unfulfilled dream of constructing an inductive logic of probabilism — the Bayesian Holy Grail — will always remain unfulfilled. Bayesian probability calculus is far from the automatic inference engine that...

Bayesianism — the new positivism No matter how atheoretical their inclination, scientists are interested in relations between properties of phenomena, not in lists of readings from dials of instruments that detect those properties … Here as elsewhere, Bayesian philosophy of science obscures a difference between scientists’ problems of hypothesis choice and the problems of prediction that are the standard illustrations and applications of probability theory....

Bayes and the ‘old evidence’ problem Among the many achievements of Newton’s theory of gravitation was its prediction of the tides and their relation to the lunar orbit. Presumably the success of this prediction confirmed Newton’s theory, or in Bayesian terms, the observable facts about the tides e raised the probability of Newton’s theory h. But the Bayesian it turns out can make no such claim. Because the facts about the tides were already known when...

The fatal flaw of mathematics .[embedded content] Gödel’s incompleteness theorems raise important questions about the foundations of mathematics. The most important concerns the question of how to select the specific systems of axioms that mathematics are supposed to be founded on. Gödel’s theorems irrevocably show that no matter what system is chosen, there will always have to be other axioms to prove previously unproved truths. This, of course, ought to...