The inhumanity of Ofqual’s algorithm

by
Frances Coppola
My articles My siteAbout meMy booksMy videos
Follow on:Twitter
Seeking Alpha

 To everyone's relief, the Government eventually caved in over the awarding of grades to A/AS level and GCSE students who had not been able to take their exams. The algorithm that awarded aspiring young people grades they did not expect and did not deserve was discarded in favour of grades set by their schools and colleges. But only if the grades awarded were too low. Those to whom the algorithm awarded over-high grades got to keep them. As a result, the rampant "grade inflation" that the Education Secretary was so desperate to prevent is now even worse than it would be if only the centre-assessed grades were used. What a mess. 

But it is not the current mess that bothers me, bad though it is. Nor even the mess there will probably be next year, when universities are faced with cramming next year's cohort into intakes already partially filled by deferrals from this year. No, it is what this algorithm tells us about the way officials at the Department of Education, OfQual and examination boards think. The  algorithm they devised has been consigned to the compost heap, but they are still there. Their inhuman reasoning will continue to influence policy for years to come.  

I say "inhuman", because for me that is what is fundamentally wrong with the "algorithm", or rather with the logical process of which the mathematical model is part. Both the model itself and its attendent processes were biased and unfair. But they are merely illustrative of the underlying - and fatal - problem. The algorithm did not treat people as individuals. It reduced them to points on a curve. It was, in short, inhuman. 

A fundamentally flawed model 

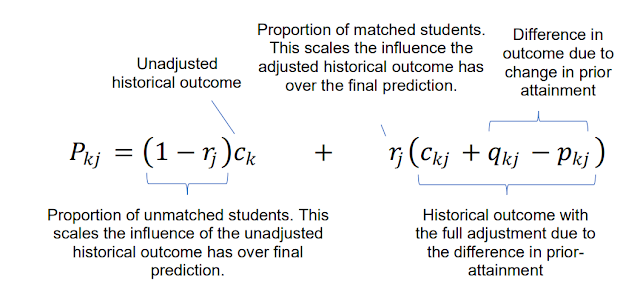
The mathematical model itself is deceptively simple. Here it is:

??? = (1 − ??)?? + ??(??? + ??? − ???) 

where Pkj is the proportion of students at the school or college allocated a particular grade in a particular subject, ckj is the historical proportion of the school or college's students that got that grade in that subject, rj is the proportion of students at the school or college for which there exists "prior attainment" data (GCSEs for A/AS levels, KS2 SATs for GCSEs), and qkj - pkj adjusts the grades awarded  to those students by the difference between their cohort's "prior attainment" and that of the 2019 cohort. The tech spec helpfully annotates the equation to this effect:

This equation will result in unfair outcomes in two dimensions. 

1. Historical performance cap

If a high proportion of students in a school or college lack "prior attainment" data in the subject under consideration, the performance of past students of that school or college will determine their grades. The predicted performance of their own cohort will make little or no difference. In the tech spec, this effect is described thus: 

From this is can be easily seen that, in a situation where a centre has no prior attainment matched students, the centre-level prediction is defined entirely by the historical centre outcome since ?? = 0 leading to the second term collapsing to zero resulting in 

{?? } = {?? }

As one mother ruefully commented on Twitter, it seemed grossly unfair that the results of her clever, hard-working younger child would be determined by the awful results achieved by her lazy, "head-in-the-clouds" older one. Of course, this algorithm doesn't operate at an individual level like that. But in aggregate, that is its effect. 

Furthermore, even when there is "prior attainment" data, the algorithm's primary reliance on historical data prevents students in the 2020 cohort from achieving grades in that subject higher than those achieved by previous cohorts in that school or college. So if the highest grade anyone ever got in biology at your school was B, that's all you could get - even if your school predicted an A* and you had a place waiting for you at Cambridge. There were stories after stories of kids at historically poorly-performing schools being awarded lower than expected grades because their predicted grade was higher than anyone had ever achieved at the school, and losing prized university places because of it. But these downgrades were not accidental. They were not a "bug" in the algorithm. They were designed into it. 

2. "Prior attainment" distortions

The algothim also created unfairness for students at schools that lacked historical data in their subjects, for example if they had not offered those subjects before, or had switched exam board or syllabus. In this case, the cjk term in the equation collapsed to zero, reducing the equation to

??? =  ??(??? − ???) 

The students' grades were entirely determined by the predicted performance of the 2020 cohort based on their GCSE results compared to those of the 2019 cohort. Why is this unfair? Because qkj - pkj was the predicted value-added performance for the whole country, not for the individual school or college. So where a school or college generally delivered higher grades than the national average across all subjects - as might be expected in selective schools, whether in the state or independent sector - students in subjects where the school or college lacked historical data were awarded grades which were far lower than might be expected, given the school's performance in other subjects.    

This actually happened at, of all places, Eton College. Here's what the Headmaster had to say about it, in a letter to parents: 

However, regrettably a number of our candidates saw their CAGs downgraded - sometimes by more than one grade and in a way in which on many occasions we feel is manifestly unfair. One particularly extreme example related to a subject in which this was the first year Eton had followed that particular syllabus and so there was no direct historic data. Rather than accept our CAGs and/or consider alternative historic data in the previous syllabus we had been following (from the same examination board), the board chose instead to take the global spread of results for 2019 and apply that to our cohort. This failed to take any account of the fact that Eton is an academically selective school with a much narrower ability range than the global spread. The results awarded to many boys in this subject bore no relation at all to their CAGs or to their ability. Several lost university places as a result. 

But the algorithm didn't just award unreasonably low grades to students at high-performing schools which lacked historical data. It also geneated spuriously low grades for high-performing schools which did have historical data. There were numerous reports of students being awarded "U" grades at schools where there had never previously been a "U" grade. How did this happen?

To understand this, it's necessary to dig a little deeper into how that "prior attainment" adjustment worked. George Constantinides explains how, for A-level students, a slightly lower GCSE profile than in previous years could generate anomalously bad results:

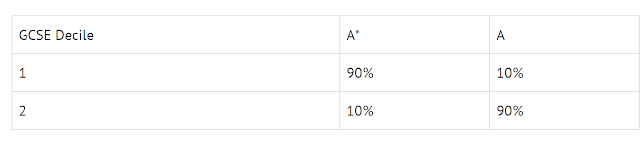
Imagine that Centre A has a historical transition matrix looking like this - all of its 200 students have walked away with A*s in this subject in recent years, whether they were in the first or second GCSE decile (and half were in each). Well done Centre A!

 Meanwhile, let's say the national transition matrix looks more like this:

 Let's now look at 2020 outcomes. Assume that this year, Centre A has an unusual cohort: all students were second decile in prior attainment. It seems natural to expect that it would still get mainly A*s, consistent with its prior performance, but this is not the outcome of the model. Instead, its historical distribution of 100% A*s is adjusted downwards because of the national transition matrix. The proportion of A*s at Centre A will be reduced by 40% - now only 60% of them will get A*s! This happens because the national transition matrix expects a 50/50 split of Decile 1 and Decile 2 students to end up with 50% A* and a Decile 2-only cohort to end up with 10% A*, resulting in a downgrade of 40%.  

George's example is, of course, highly simplified. But in this lovely interactive visualisation, Tom SF Haines shows how, under the same circumstances, some poor beggar at a high-performing school could end up with a "U" grade even if they were predicted an A. Here's his scenario: 

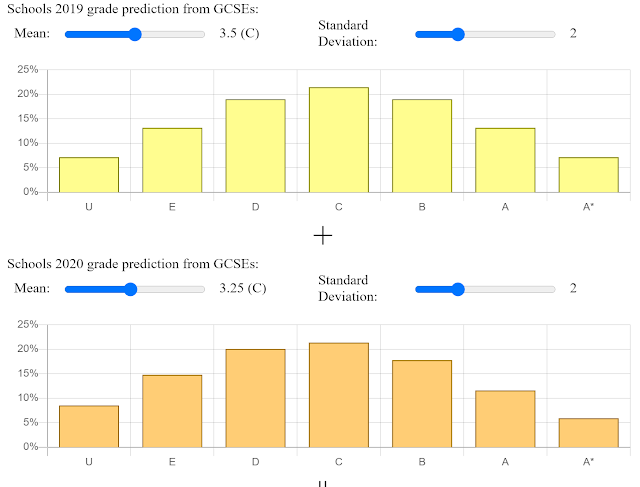
Imagine a truly spectacular school - half the students get A* and less than 1% of students get a C. It does this despite getting entirely normal students, and this year they are very slightly worse: Just a quarter of a grade less than normal based on GCSE results. That could be nothing more than road works outside on exam day. 

Here's the historical grade distribution for his "brilliant" school:

The algorithm then takes the "prior attainment" distributions for 2019 and 2020 for the school and generates predicted grades for them as if the school followed the national profile of grade distribution. For this example, with slightly poorer GCSE results in 2020 than 2019, the results are as follows:

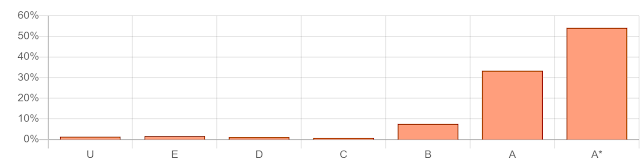
You'd be wrong:

The "prior attainment" part of the algorithm has applied the national grade distribution to the predicted results of this school. The school's strong historical performance supports the grades of stronger candidates, but middle grades are crushed and weaker candidates are pushed down the grade distribution. The weakest in the class fails their A-level.  

By applying the national 2019-2020 value-added distribution instead of schools' own, the algorithm forces down the results of weaker candidates at high-performing schools. It also forces up the results of stronger candidates at low-performing schools, but as already noted, the historical data cap prevents these students being given grades higher than their school's previous highest grade. So the overall effect of the algorithm is to depress grades across the board. 

There can be no doubt that this was intentional. The commentary in the tech spec recognises that most schools don't follow the national grade distribution - indeed its own example uses a school that out-performs the national distribution. But it then says this:

Due to the differential nature of the calculations that follow, these effects are removed when forming the actual prediction for the centre this year.

The curve is everything. Squash the outliers. 

Squash the outliers - but not in the historical data 

The fact that the national "prior attainment" profile, rather than the school's own, was used to generate predicted results might also explain why a generally high-performing school with occasional lapses from grace could end up with bad results for 2020. But there is another reason too - and that is the way in which the data feeding into the algorithm was prepared.

Since the algorithm was designed to suppress outliers, particularly but not exclusively at the top end of the distribution, we might expect that Ofqual would instruct examination boards to remove outliers from historical data. But it didn't. So a single "U" grade in a school or college's historical data was allowed to influence its entire historical data profile. Of course, this could mean better results for some schools. But for others, it could result in unusually bad results. Across schools and colleges as a whole, failing to eliminate outliers from historical data while suppressing high performers in the current cohort would result in an unusually large number of schools delivering poorer results than usual. Anecdotally, this seems to be what has happened. 

When I pointed this out on Twitter, a few people took me to task for wanting outliers removed: "These are real children!" they said. But if removing outliers in historical data is unacceptable because they are the exam results of real children, then so too is suppressing outliers in current results. After all, those are real children too. And unlike the historical outliers, who would have been entirely unaffected by a decision to remove them from the data, the outliers in the current data would have suffered life-long consequences from Ofqual's decision to suppress them.  

Adding unfairness in the name of "fairness"

The tech spec recognises that the results of small groups of students can't be fitted to a statistical curve. Every HR professional knows this, of course: performance appraisals for a department of 200 might approximate to a bell curve, but forcing the appraisals for a team of 5 on to a bell curve results in robbing Peter to pay Paul. But the solution that the Ofqual designers came up with was not only fundamentally unfair, it resulted in actual discrimination against children from disadvantaged backgrounds and, almost certainly, BAME children. How the Ofqual team managed to miss this is beyond belief.  

The Ofqual team's solution to the "small cohort" problem was to use teacher-assessed grades instead of the algorithm. They seem to have decided that it was better to tolerate some grade inflation than try to use a statistical model to generate grades for students in small classes. So they applied teacher-assessed grades (CAGs) entirely for groups of 5 students or less, and partially for groups of 6-14 students, gradually reducing the weight given to CAGs as the group size increased. Large groups, defined as 15 students or more, would be entirely algorithm-assessed. 

You'd think, wouldn't you, that by "group" they would mean the number of students taking a particular subject at a particular school or centre in 2020. But no. They decided that "group" would mean the average number of students taking that subject at the school or centre across the entire period for which they had historic data. And the average they took wasn't exactly straightforward either - none of this "mean" or "median" nonsense. They used the "harmonic mean" - the reciprocal of the reciprocals. As George Constantinides explains, this meant that a group as small as 8 could be designated as "large" and entirely algo-assessed, if at some time in the past there had been a much larger group. 

The students who received teacher-assessed grades were generally these: 

• students studying minority subjects such as music or Latin (though a signifcant proportion of these were algo-assessed, perhaps because of the dubious definition of "group")
• students in smaller schools

Since smaller schools and minority subjects are disproportionately found in the private sector, the exception effectively discriminated in their favour. But once again, the real problem here was not the effective discrimination in favour of private schools, bad though this was. It was the mindset among those devising this algorighm and authorising its use. The tech spec emphasises "faiarness" throughout. But the design team were were apparently unable to see the intrinsic unfairness of assessing students studying the same subject in two fundamentally different ways, one of which is known to be more generous than the other, simply on the basis of the size of school they attended. Or if they did see it, they didn't care.  

Whether through incompetence, malevolence or some combination of both, the fact is that the designers of this algorithm were willing to sacrifice the future careers of real young people on the altar of a desired grade distribution. And to add insult to injury, they then introduced systematic discrimination into their unethical design in the name of "fairness". 

How Ofqual lost the plot

At this point, it's worth reminding ourselves what purpose the algorithm and associated processes were supposed to serve.

Because of the pandemic, the government cancelled external exams for GCSE, A/AS level, BTEC and certain other national qualifications. The algorithm was supposed to provide a credible alternative to examination results so that universities and colleges could honour offers already made and employers could make offers to school leavers. Examinations, of course, have always measured individual performance. But Ofqual's algorithm discarded individual performance in favour of profiling candidates in relation to a group standard. It was a fine example of what is known as the "ecological fallacy": the flawed notion that the characteristics of an individual can be deduced from the characteristics of the group of which they are part.  

Of course, exams are deeply flawed and in many ways unfair. Very talented candidates can perform badly on the day for a variety of reasons. Examination papers are something of a lottery, since they can only cover a small proportion of the material studied: teachers and candidates try to second-guess the subjects that will come up in an examination in the hope of focusing their revision on the right areas. It doesn't always work: I still remember opening the second paper in my biology A-level and finding that the very first question was on a subject that we had not even studied, let alone revised. Exams notoriously vary in difficulty year-by-year, so grade boundaries are statistically adjusted to maintain roughly equivalent proportions of candidates at each grade. And examiners are flawed individuals who don't necessarily mark to common standards, and even when they do, don't necessarily agree on what the answer should be. If only we could find some better way of establishing how good someone is at a subject they have studied. 

But Ofqual wasn't asked to find a "fairer" or "better" way of assessing individual performance. It was tasked with moderating and standardising CAGs to make them as much like the missing exam results as possible. It appears to have completely lost sight of this objective. And as a result, it spectacularly failed to achive it. The algorithm's grade awards come nowhere near replicating exam results. 

To be fair, neither do the CAGs to which we are now reverting. All we have done is replace a flawed algorithm with flawed assessments. Teachers are every bit as fallible as examiners: they can be racist, sexist, ableist, or simply dislike a particular student. And "teacher's pets" exist. The process that schools and colleges went through to assess grades to replace those the students would have been awarded in exams was in most cases extremely rigorous, involving layer upon layer of checks and balances: but in the end it was still a subjective assessment by people who knew the students.

Ofqual was convinced - with some justification - that if teacher assessments replaced exam grades, there would be considerable "grade inflation". It was only mandated by the Department of Education to avoid grade inflation "to the extent possible." But its zeal to avoid grade inflation led it down a dangerous and ultimately futile path,  Instead of moderating and standardising the CAGs, it abandoned them. And instead of assessing individuals independently as exams do, it eliminated them.   

And in so doing, it created a system that was even more unfair than the exams and the teacher assessments it eliminated. After all, at least those attempted to assess students' own performance. But the algorithm assessed student's performance solely by reference to other, unrelated, people's performance, at a different time and in a different place. All the work that the students themselves put in counted for nothing. Even their own prior attainment was deliberately ignored: 

It is important to note that neither through the standardisation process applied this year nor the use of cohort level predictions in a typical year, does a student’s individual prior attainment dictate their outcome in a subject. Measures of prior-attainment are only used to characterise and, therefore, predict for group relationships between students.

Those who designed this inhuman system thought they could behave like gods, deciding at the throw of a dice who should succeed and who should fail, and caring nothing for the young lives they would ruin. "If a few teenagers don't get their university places, too bad." 

But they are not gods. They are our servants. And they need cutting down to size. This fiasco has ended unsatisfactorily, but at least no-one was killed. But it's not beyond the bounds of possibility that a future algorithm might make life or death decisions about individuals based on historical data not about them, but about other people deemed to be "like them". We must not go any further down this path. Let the examinations disaster serve as an awful warning. Never again should the designers of algorithms be given sole responsibility for making decisions about individuals that will change their lives forever.