The limits of probabilistic reasoning Probabilistic reasoning in science — especially Bayesianism — reduces questions of rationality to questions of internal consistency (coherence) of beliefs, but, even granted this questionable reductionism, it’s not self-evident that rational agents really have to be probabilistically consistent. There is no strong warrant for believing so. Rather, there is strong evidence for us encountering huge problems if we let probabilistic reasoning become the dominant method for doing research in social sciences on problems that involve risk and uncertainty. In many of the situations that are relevant to economics, one could argue that there is simply not enough of adequate and relevant information to ground beliefs of a
Topics:
Lars Pålsson Syll considers the following as important: Statistics & Econometrics
This could be interesting, too:
Lars Pålsson Syll writes Keynes’ critique of econometrics is still valid
Lars Pålsson Syll writes The history of random walks
Lars Pålsson Syll writes The history of econometrics
Lars Pålsson Syll writes What statistics teachers get wrong!
The limits of probabilistic reasoning
Probabilistic reasoning in science — especially Bayesianism — reduces questions of rationality to questions of internal consistency (coherence) of beliefs, but, even granted this questionable reductionism, it’s not self-evident that rational agents really have to be probabilistically consistent. There is no strong warrant for believing so. Rather, there is strong evidence for us encountering huge problems if we let probabilistic reasoning become the dominant method for doing research in social sciences on problems that involve risk and uncertainty.
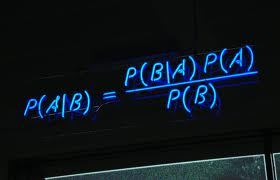 In many of the situations that are relevant to economics, one could argue that there is simply not enough of adequate and relevant information to ground beliefs of a probabilistic kind and that in those situations it is not possible, in any relevant way, to represent an individual’s beliefs in a single probability measure.
In many of the situations that are relevant to economics, one could argue that there is simply not enough of adequate and relevant information to ground beliefs of a probabilistic kind and that in those situations it is not possible, in any relevant way, to represent an individual’s beliefs in a single probability measure.
Say you have come to learn (based on own experience and tons of data) that the probability of you becoming unemployed in Sweden is 10%. Having moved to another country (where you have no own experience and no data) you have no information on unemployment and a fortiori nothing to help you construct any probability estimate on. A Bayesian would, however, argue that you would have to assign probabilities to the mutually exclusive alternative outcomes and that these have to add up to 1 if you are rational. That is, in this case – and based on symmetry – a rational individual would have to assign probability 10% to become unemployed and 90% to become employed.
That feels intuitively wrong though, and I guess most people would agree. Bayesianism cannot distinguish between symmetry-based probabilities from information and symmetry-based probabilities from an absence of information. In these kinds of situations, most of us would rather say that it is simply irrational to be a Bayesian and better instead to admit that we “simply do not know” or that we feel ambiguous and undecided. Arbitrary an ungrounded probability claims are more irrational than being undecided in face of genuine uncertainty, so if there is not sufficient information to ground a probability distribution it is better to acknowledge that simpliciter, rather than pretending to possess a certitude that we simply do not possess.
I think this critique of Bayesianism is in accordance with the views of John Maynard Keynes’ A Treatise on Probability (1921) and General Theory (1937). According to Keynes we live in a world permeated by unmeasurable uncertainty – not quantifiable stochastic risk – which often forces us to make decisions based on anything but rational expectations. Sometimes we “simply do not know.” Keynes would not have accepted the view of Bayesian economists, according to whom expectations “tend to be distributed, for the same information set, about the prediction of the theory.” Keynes, rather, thinks that we base our expectations on the confidence or ‘weight’ we put on different events and alternatives. To Keynes expectations are a question of weighing probabilities by ‘degrees of belief,’ beliefs that have preciously little to do with the kind of stochastic probabilistic calculations made by the rational agents modelled by probabilistically reasoning Bayesian economists.
We always have to remember that economics and statistics are two quite different things, and as long as economists cannot identify their statistical theories with real-world phenomena there is no real warrant for taking their statistical inferences seriously.
Just as there is no such thing as a ‘free lunch,’ there is no such thing as a ‘free probability.’ To be able at all to talk about probabilities, you have to specify a model. If there is no chance set-up or model that generates the probabilistic outcomes or events -– in statistics one refers to any process where you observe or measure as an experiment (rolling a die) and the results obtained as the outcomes or events (number of points rolled with the die, being e. g. 3 or 5) of the experiment -– there, strictly seen, is no event at all.
Probability is a relational element. It always must come with a specification of the model from which it is calculated. And then to be of any empirical scientific value it has to be shown to coincide with (or at least converge to) real data generating processes or structures –- something seldom or never done in economics.
And this is the basic problem!
If you have a fair roulette-wheel, you can arguably specify probabilities and probability density distributions. But how do you conceive of the analogous ‘nomological machines’ for prices, gross domestic product, income distribution etc? Only by a leap of faith. And that does not suffice in science. You have to come up with some really good arguments if you want to persuade people into believing in the existence of socio-economic structures that generate data with characteristics conceivable as stochastic events portrayed by probabilistic density distributions! Not doing that, you simply conflate statistical and economic inferences.
The present ‘machine learning’ and ‘big data’ hype shows that many social scientists — falsely — think that they can get away with analysing real-world phenomena without any (commitment to) theory. But — data never speaks for itself. Without a prior statistical set-up, there actually are no data at all to process. And — using a machine learning algorithm will only produce what you are looking for. Theory matters.
Causality in social sciences — and economics — can never solely be a question of statistical inference. Causality entails more than predictability, and to really in-depth explain social phenomena require theory. Analysis of variation — the foundation of all econometrics — can never in itself reveal how these variations are brought about. First when we are able to tie actions, processes or structures to the statistical relations detected, can we say that we are getting at relevant explanations of causation. Most facts have many different, possible, alternative explanations, but we want to find the best of all contrastive (since all real explanation takes place relative to a set of alternatives) explanations. So which is the best explanation? Many scientists, influenced by statistical reasoning, think that the likeliest explanation is the best explanation. But the likelihood of x is not in itself a strong argument for thinking it explains y. I would rather argue that what makes one explanation better than another are things like aiming for and finding powerful, deep, causal, features and mechanisms that we have warranted and justified reasons to believe in. Statistical — especially the variety based on a Bayesian epistemology — reasoning generally has no room for these kinds of explanatory considerations. The only thing that matters is the probabilistic relation between evidence and hypothesis. That is also one of the main reasons I find abduction — inference to the best explanation — a better description and account of what constitute actual scientific reasoning and inferences.
Most facts have many different, possible, alternative explanations, but we want to find the best of all contrastive (since all real explanation takes place relative to a set of alternatives) explanations. So which is the best explanation? Many scientists, influenced by statistical reasoning, think that the likeliest explanation is the best explanation. But the likelihood of x is not in itself a strong argument for thinking it explains y. I would rather argue that what makes one explanation better than another are things like aiming for and finding powerful, deep, causal, features and mechanisms that we have warranted and justified reasons to believe in. Statistical — especially the variety based on a Bayesian epistemology — reasoning generally has no room for these kinds of explanatory considerations. The only thing that matters is the probabilistic relation between evidence and hypothesis. That is also one of the main reasons I find abduction — inference to the best explanation — a better description and account of what constitute actual scientific reasoning and inferences.
And even worse — some economists using statistical methods think that algorithmic formalisms somehow give them access to causality. That is, however, simply not true. Assuming ‘convenient’ things like ‘faithfulness’ or ‘stability’ is to assume what has to be proven. Deductive-axiomatic methods used in statistics do no produce evidence for causal inferences. The real causality we are searching for is the one existing in the real world around us. If there is no warranted connection between axiomatically derived statistical theorems and the real-world, well, then we haven’t really obtained the causation we are looking for.
