by Expected utility theory and ergodicity — poor guides to decision-making Behavioural scientists generally explore decision making using simple gambles with “additive dynamics.” In each gamble, a person wins or loses fixed amounts of money – say, gaining £1 for a win, and losing £0.50 for a loss. Gambles of this kind turn out to be “ergodic” in the sense that averages over the possible outcomes really are equal to averages over time if the gamble is played many times. Because of this, using Expected Utility Theory with a linear utility function – utility simply being proportional to the amount won or lost – turns out to be optimal for maximising the growth of wealth over time. But this additive paradigm isn’t a useful model for many real-world decisions
Topics:
Lars Pålsson Syll considers the following as important: Economics
This could be interesting, too:
Lars Pålsson Syll writes Klas Eklunds ‘Vår ekonomi’ — lärobok med stora brister
Lars Pålsson Syll writes Ekonomisk politik och finanspolitiska ramverk
Lars Pålsson Syll writes NAIRU — a harmful fairy tale
Lars Pålsson Syll writes Isabella Weber on sellers inflation
Expected utility theory and ergodicity — poor guides to decision-making
Behavioural scientists generally explore decision making using simple gambles with “additive dynamics.” In each gamble, a person wins or loses fixed amounts of money – say, gaining £1 for a win, and losing £0.50 for a loss. Gambles of this kind turn out to be “ergodic” in the sense that averages over the possible outcomes really are equal to averages over time if the gamble is played many times.
Because of this, using Expected Utility Theory with a linear utility function – utility simply being proportional to the amount won or lost – turns out to be optimal for maximising the growth of wealth over time.
But this additive paradigm isn’t a useful model for many real-world decisions where the amount gained or lost in a gamble depends on how much wealth an individual already has … Many gambles with positive expectation values – seemingly worth playing from the EUT perspective – actually yield consistent losses when played out in time. In situations with multiplicative dynamics, it turns out that one can still use the EUT framework, but only if the utility is considered to depend logarithmically on the outcome.
This implies that the actually optimal behaviour depends very sensitively on the nature of the gamble dynamics. Or, in the setting of EUT, that the utility a person assigns to an outcome – winning £1, for example – should change if the gamble flips between additive and multiplicative dynamics. If people really act this way, it’s a big problem for both expected utility theory and prospect theory which assert that utility functions should be fixed and stable, indifferent to dynamics.
Suppose I want to play a game. Let’s say we are tossing a coin. If heads comes up, I win a dollar, and if tails comes up, I lose a dollar. Suppose further that I believe I know that the coin is asymmetrical and that the probability of getting heads (p) is greater than 50% – say 60% (0.6) – while the bookmaker assumes that the coin is totally symmetric. How much of my bankroll (T) should I optimally invest in this game?
A strict mainstream utility-maximizing economist would suggest that my goal should be to maximize the expected value of my bankroll (wealth), and according to this view, I ought to bet my entire bankroll.
Does that sound rational? Most people would answer no to that question. The risk of losing is so high, that I already after few games played — the expected time until my first loss arises is 1/(1-p), which in this case is equal to 2.5 — with a high likelihood would be losing and thereby become bankrupt. The expected-value maximizing economist does not seem to have a particularly attractive approach.
So what’s the alternative? One possibility is to apply the so-called Kelly criterion — after the American physicist and information theorist John L. Kelly, who in the article A New Interpretation of Information Rate (1956) suggested this criterion for how to optimize the size of the bet — under which the optimum is to invest a specific fraction (x) of wealth (T) in each game. How do we arrive at this fraction?
When I win, I have (1 + x) times as much as before, and when I lose (1 – x) times as much. After n rounds, when I have won v times and lost n – v times, my new bankroll (W) is
(1) W = (1 + x)v(1 – x)n – v T
(A technical note: The bets used in these calculations are of the “quotient form” (Q), where you typically keep your bet money until the game is over, and a fortiori, in the win/lose expression it’s not included that you get back what you bet when you win. If you prefer to think of odds calculations in the “decimal form” (D), where the bet money typically is considered lost when the game starts, you have to transform the calculations according to Q = D – 1.)
The bankroll increases multiplicatively — “compound interest” — and the long-term average growth rate for my wealth can then be easily calculated by taking the logarithms of (1), which gives
(2) log (W/ T) = v log (1 + x) + (n – v) log (1 – x).
If we divide both sides by n we get
(3) [log (W / T)] / n = [v log (1 + x) + (n – v) log (1 – x)] / n
The left hand side now represents the average growth rate (g) in each game. On the right-hand side the ratio v/n is equal to the percentage of bets that I won, and when n is large, this fraction will be close to p. Similarly, (n – v)/n is close to (1 – p). When the number of bets is large, the average growth rate is
(4) g = p log (1 + x) + (1 – p) log (1 – x).
Now we can easily determine the value of x that maximizes g:
(5) d [p log (1 + x) + (1 – p) log (1 – x)]/d x = p/(1 + x) – (1 – p)/(1 – x) =>
p/(1 + x) – (1 – p)/(1 – x) = 0 =>
(6) x = p – (1 – p)
Since p is the probability that I will win, and (1 – p) is the probability that I will lose, the Kelly strategy says that to optimize the growth rate of your bankroll (wealth) you should invest a fraction of the bankroll equal to the difference of the likelihood that you will win or lose. In our example, this means that I have in each game to bet the fraction of x = 0.6 – (1 – 0.6) ≈ 0.2 — that is, 20% of my bankroll. Alternatively, we see that the Kelly criterion implies that we have to choose x so that E[log(1+x)] — which equals p log (1 + x) + (1 – p) log (1 – x) — is maximized. Plotting E[log(1+x)] as a function of x we see that the value maximizing the function is 0.2:
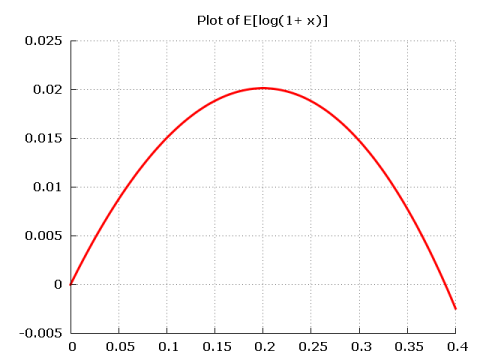
The optimal average growth rate becomes
(7) 0.6 log (1.2) + 0.4 log (0.8) ≈ 0.02.
If I bet 20% of my wealth in tossing the coin, I will after 10 games on average have 1.0210 times more than when I started (≈ 1.22).
This game strategy will give us an outcome in the long run that is better than if we use a strategy building on the mainstream theory of choice under uncertainty (risk) – expected value maximization. If we bet all our wealth in each game we will most likely lose our fortune, but because with low probability we will have a very large fortune, the expected value is still high. For a real-life player – for whom there is very little to benefit from this type of ensemble-average – it is more relevant to look at time-average of what he may be expected to win (in our game the averages are the same only if we assume that the player has a logarithmic utility function). What good does it do me if my tossing the coin maximizes an expected value when I might have gone bankrupt after four games played? If I try to maximize the expected value, the probability of bankruptcy soon gets close to one. Better then to invest 20% of my wealth in each game and maximize my long-term average wealth growth!
When applied to the mainstream theory of expected utility, one thinks in terms of “parallel universe” and asks what is the expected return of an investment, calculated as an average over the “parallel universe”? In our coin toss example, it is as if one supposes that various “I” are tossing a coin and that the loss of many of them will be offset by the huge profits one of these “I” does. But this ensemble-average does not work for an individual, for whom a time-average better reflects the experience made in the “non-parallel universe” in which we live.
The Kelly criterion gives a more realistic answer, where one thinks in terms of the only universe we actually live in, and ask what is the expected return of an investment, calculated as an average over time.
Since we cannot go back in time — entropy and the “arrow of time ” make this impossible — and the bankruptcy option is always at hand (extreme events and “black swans” are always possible) we have nothing to gain from thinking in terms of ensembles and “parallel universe.”
Actual events follow a fixed pattern of time, where events are often linked in a multiplicative process (as e. g. investment returns with “compound interest”) which is basically non-ergodic.
Instead of arbitrarily assuming that people have a certain type of utility function – as in mainstream theory – the Kelly criterion shows that we can obtain a less arbitrary and more accurate picture of real people’s decisions and actions by basically assuming that time is irreversible. When the bankroll is gone, it’s gone. The fact that in a parallel universe it could conceivably have been refilled, are of little comfort to those who live in the one and only possible world that we call the real world.
Our coin toss example can be applied to more traditional economic issues. If we think of an investor, we can basically describe his situation in terms of our coin toss. What fraction (x) of his assets (T) should an investor – who is about to make a large number of repeated investments – bet on his feeling that he can better evaluate an investment (p = 0.6) than the market (p = 0.5)? The greater the x, the greater is the leverage. But also – the greater is the risk. Since p is the probability that his investment valuation is correct and (1 – p) is the probability that the market’s valuation is correct, it means the Kelly criterion says he optimizes the rate of growth on his investments by investing a fraction of his assets that is equal to the difference in the probability that he will “win” or “lose.” In our example this means that he at each investment opportunity is to invest the fraction of x = 0.6 – (1 – 0.6), i.e. about 20% of his assets. The optimal average growth rate of investment is then about 2 % (0.6 log (1.2) + 0.4 log (0.8)).
Kelly’s criterion shows that because we cannot go back in time, we should not take excessive risks. High leverage increases the risk of bankruptcy. This should also be a warning for the financial world, where the constant quest for greater and greater leverage — and risks – creates extensive and recurrent systemic crises. A more appropriate level of risk-taking is a necessary ingredient in a policy to come to curb excessive risk-taking .
The works of people like Kelly and Ole Peters at London Mathematical Laboratory show that expected utility theory is transmogrifying truth. Economics needs something different than a theory relying on arbitrary utility functions.