Probability for geeks

by
Frances Coppola
My articles My siteAbout meMy booksMy videos
Follow on:Twitter
Seeking Alpha

But there are dissenting voices. For example, in this piece, Jonald Fyookball disputes the claims of the Lightning enthusiasts on the grounds that the mathematics doesn't stack up. Predictably, the Lightning geeks have fought back: the pseudonymous "Murch", a software engineer at the Bitgo cryptocurrency exchange, describes Fyookball's analysis as "laughable".

Fyookball describes the Lightning network thus:

To send or receive bitcoins, you need either a payment channel with that specific user, or a linked series of payment channels (a “route”).

It’s pointless to create a payment channel for the sole purpose of sending an off-chain transaction, since it requires an on-chain transaction to open the channel (and another one to close). You might as well just send an on-chain transaction instead; you don’t need the LN. 

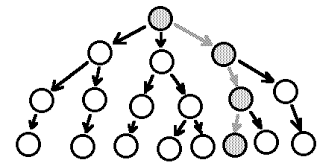
The idea is that you’re supposed to be able to route your payment to any destination through a series of connections. From the viewpoint of a user, the potential path to anyone else looks like a tree structure:

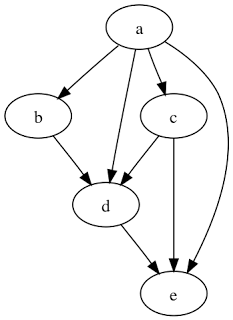
When a LN participant searches for a route, they're obviously only interested in directed payment capacity. This aspect is correctly represented in the tree. However, the nodes along the route are interconnected. While this could even allow cycles to occur, cycles are not possible in the route construction, as it would allow participants involved multiple times to cut out the cycle when learning the secret for the first time. The resulting graph is what we call a DAG or directed acyclic graph:

To explain, let's look at how Lightning decision-making works. We need a whole cast of actors, not just the famous Carol and Bob. Lightning is supposed to be used for small transactions, so let's imagine that Alice wants to buy a coffee in Starbucks. She doesn't have an open Lightning channel with Starbucks (we could call it an "account"), so she asks her friend Carol to pay Starbucks for her, and she will reimburse Carol when the payment is made. Carol doesn't have an open channel either, so she asks Bob to pay Starbucks. Bob has an open channel with Starbucks, so he makes the payment and is reimbursed by Carol, who can then claim her payment from Alice. This looks like a tree structure, doesn't it?

No. Each of the actors has more than one relationship. Alice could have asked Tim or Jim to make the payment for her. Why did she choose Carol? Well, there might be all number of reasons. Perhaps she wrongly thought Carol had an open Starbucks channel. Perhaps Tim was away on holiday and she wasn't able to contact him. Perhaps Alice simply issued a broadcast message to all her friends and Carol was the first to answer. Perhaps Carol was simply the first person to come into Alice's mind. There are all manner of reasons why people might choose a particular participant.

Carol, too, has more than one relationship. Why did she choose Bob? We don't know. And importantly, Alice doesn't know. When Alice asks Carol to pay Starbucks, she does not know what payment route Carol will choose. Carol doesn't have to send that payment directly. Indeed, if she doesn't have an open Starbucks channel, she can't. So she sends it via Bob. But she could have chosen Tim or Jim instead. Yes, the same Tim and Jim that Alice also knows. And if Bob knows them too, then he could route the payment via Tim or Jim instead of paying Starbucks directly. The structure is therefore not just a simple tree structure.

But more importantly, none of the participants knows the route in advance. Each participant has a number of choices, and no participant knows what choices the other participants will make. The final route is therefore not determined until Starbucks gets its money and the payment cascade back to Alice starts. And because no-one knows what anyone else will do, the final route is randomly determined.

Murch disputes this, so let me explain. If we assume that all participants are equal (which is necessary for full decentralisation), then the more potential participants there are, the greater the number of potential routes, and the lower the probability that a given route will be the final one. When there are only a very small number of potential participants, then the probabilities can be calculated. But when the network expands to thousands or millions, as Lightning enthusiasts intend, then the number of potential routes rises exponentially, and the probability of any one route being selected approaches zero. Obviously, one route will be selected: but the selection is effectively random.

Murch's argument is that everyone will know their friends, so the choice of route would not be random. I'm afraid this is our old friend the fallacy of composition, otherwise known as "generalising from the particular". I know my friends, and I may know some of their friends: but I don't know their friends' friends, let alone their friends' friends' friends. Once we are more than about one or two steps removed from the originator's circle of friends, the originator simply does not know enough about the network to be able to predict what direction the payment route will take. Nor does any other participant. The more potential participants there are, and the more choices each participant has, the less knowledge anyone will have about what is really going on.

Payment routes could become very long and very complex without anyone knowing. They could even become recursive. Because this is a DAG not a tree structure, it is entirely possible that the same person could be asked to make a payment more than once in the same chain, by two different participants. Murch says this isn't possible, but unless there is some kind of Fat Controller preventing duplicate participation in payment chains, he is wrong. Anyone can choose their participants, and people only see their own backyards, so it is absolutely possible for a payment to be sent twice to the same participant, and no-one would know.

But why might a simple payment to Starbucks become so complex? Well, this brings me to the second area of dispute between Fyookball and Murch. Fyookball describes Lightning payments as "lending". Murch says they are nothing of the kind: they are simply a balance trade. Who is right?

This time, Fyookball is right. Lightning is a "pull" system. Every participant makes a payment, then "pulls" reimbursement from the previous participant. So each participant has to have sufficient "own funds" in their channel to make the payment. If they don't, they can't participate in the route, and their predecessor must find a different participant. Using "own funds" to make a payment on behalf of someone else meets the normal definition of "lending". It may be settled within milliseconds (or not, as we shall see), but that doesn't change what it is.

Note also that no-one gets paid until Starbucks does. Carol cannot claim her payment from Alice until Bob claims his payment from her, and Bob cannot claim his payment from Carol until Starbucks claims its payment from him. The final payment in the route triggers a cascade of claims. When there are a lot of hops in the route, therefore, reimbursement for early participants could be significantly delayed.

Reimbursement delays could seriously degrade network performance. When a participant commits to a payment, the "own funds" in the channel must be available for that payment. But any funds already committed to another payment that hasn't yet settled are not available. We can think of this as like selling your house: if you've already exchanged contracts with someone, but the sale hasn't completed because there is a blockage further up the chain, you can't sell your house to someone else. If there are insufficient unencumbered funds in the channel, the participant can't commit to the payment, and the channel becomes "unresponsive". When network traffic is heavy, then if all participants are small users with limited funds, it is possible that all potential payment routes available to a particular participant could become unresponsive, resulting in payments failing to complete. That is gridlock.

And if you think this couldn't happen, you need to play The London Game. In this, players ride London's Tube system to reach various randomly-determined tourist destinations. You start at a major London train station, and you use the Tube map to work out how to get to your destination. Note that this is already significantly less difficult than the Lightning system, because at least you can see the whole map and work out a viable route. In Lightning, you can't see more than a couple of Tube stops beyond your start point.

But your route choices are immediately compromised by two things; the decisions of other players regarding which Tube stops should be closed (become unresponsive, in Lightning parlance), and the Hazard cards that mean you can be randomly diverted somewhere else (this approximates to losing control of your route, as you do in Lightning). Let's suppose you are trying to get from Victoria to Tower Hill, and someone decides to close Embankment. I've put a London Tube map at the head of this post so you can amuse yourself working out what effect that has on what was quite a short, simple route. Or let's suppose you were trying to get from Liverpool Street to Regent's Park, but you get diverted by a Hazard card and end up at Temple, again with Embankment closed. It's not difficult to see that available routes quickly become long, complex and congested - and this is with only one closed Tube stop. As more Tube stops are closed, it is actually possible for some participants to be completely unable to move: for example, if you are at St. James's Park and someone closes both Victoria and Westminster, you aren't going anywhere.

Gridlock is, of course, the fun of The London Game. But when it occurs in a payments system (or on the Tube in reality, of course) it is anything but fun.

Now, of course the London Tube is not a fully decentralised system. All tube stops are not equal. Taking out Oxford Circus has a far more disruptive effect on network traffic than taking out Swiss Cottage. Lightning at least attempts to level the playing field, but it does so at the price of inevitable gridlock. The combination of low funds levels in payment channels with payment delays due to long chains is deadly.

And Lightning has a second problem, too. Because players of The London Game can see the whole map, they spend much of their time working out alternative routes. But Lightning users can't see the whole map. All they can do is try different payment channels. Their situation is rather similar to a Tube user, knowing that Westminster is blocked, deciding to go via Oxford Circus instead, only to discover at Green Park that Oxford Circus is blocked too. The fact that no-one knows either the past or the future of a payment route creates the real possibility that some payments may never reach their destination at all, but wander the network forever like the Flying Dutchman.

Suppose that Alice's payment fails to settle. It hops from participant to participant, but no-one ever sends it to Starbucks. How does this look to the participants? Well, Carol, Bob, Tim, Jim, Old Uncle Tom Cobbleigh and all lose money, because they make payments for which they are never reimbursed. None of them know why the payment fails to settle, because all they can see is their own back yard. They don't realise that the problem is that no-one has a channel with Starbucks, or if they have one, they either can't or don't want to use it. So they mutter about funds being "stolen". And Alice may face a lawsuit from Starbucks for failing to pay for her coffee.

Because this is a network, there is absolutely nothing any of them can do to stop the payment wandering, except by opening a channel with Starbucks - and why would they do that for a one-off payment? Individually, their decisions not to send the payment to Starbucks are no doubt entirely rational. But collectively, their behaviour results in a payment failure. This is what Fyookball means when he refers to the possibility that there may not be a path at all.

But is Fyookball's solution any better? Well, having dedicated payment channels with much larger reserves that remained online all the time would ease Lightning's liquidity problem, and if liquidity was more abundant there might be less likelihood that payments would seize up or "wander". People would simply send their payment to a liquidity hub, which would maintain a permanently open channel with Starbucks. But this could hardly be called "decentralised". The liquidity hub would inevitably be a target for thieves and hackers. And if it went down, the network could have a heart attack, just as closing Oxford Circus brings the entire London Tube network to a halt (believe me, it does).

Of course, Lightning is a financial system, not a transport network. So perhaps we should call such a centralised payment channel by a different name. "Lehman Brothers", for example. How does that sound?

Related reading:

Thunder and lightning in the Bitcoin world - Forbes
Pilate's Game
Calculus for journalists
Tweet thread on Lightning