by Gabriel Sterne complains about economists' loose use of mathematical terminology: Of course, it's not just economists who use "increase" and "accelerate" interchangeably. But economics is a mathematical discipline, and in mathematics, "increase" and "accelerate" mean different things. So is Gabriel's observation true, and if it is, is it a problem?To test Gabriel's hypothesis, I ran a little Twitter test. I asked this question: This was of course far from rigorous: the sample was self-selecting, there was no way of restricting it to economists (though I did ban finance tweeps from answering), and it all depended who was on Twitter this morning. And the terminology I used was itself confusing - deliberately so, since this is how economists often write. But the results were nevertheless
Topics:
Frances Coppola considers the following as important: Economics, Hyperinflation, inflation, mathematics
This could be interesting, too:
Lars Pålsson Syll writes The non-existence of economic laws
Lars Pålsson Syll writes Cutting-edge macroeconomics …
Lars Pålsson Syll writes Tourism — a critical perspective
Matias Vernengo writes The Argentina of Javier Milei
Gabriel Sterne complains about economists' loose use of mathematical terminology:
Of course, it's not just economists who use "increase" and "accelerate" interchangeably. But economics is a mathematical discipline, and in mathematics, "increase" and "accelerate" mean different things. So is Gabriel's observation true, and if it is, is it a problem?
To test Gabriel's hypothesis, I ran a little Twitter test. I asked this question:
This was of course far from rigorous: the sample was self-selecting, there was no way of restricting it to economists (though I did ban finance tweeps from answering), and it all depended who was on Twitter this morning. And the terminology I used was itself confusing - deliberately so, since this is how economists often write.
But the results were nevertheless interesting. Most non-economists got the answer right. Physicists, in particular, understood it straight away. But most economists who answered got it wrong.
As the title of this post indicates, we are back in the realms of calculus again. So I'm going to do something I couldn't really do on Twitter, namely define my terms, starting with what I mean by "inflation." At this point, any goldbugs reading this post can leave the room. Inflation on this occasion has nothing to do with the money supply.
We define inflation as the rate of increase of the price level. It is therefore the first derivative of the price level P with respect to time, t. We express this mathematically as dP/dt.
The fact that inflation is the first derivative of price with respect to time is, I think, the reason why economists get this wrong but others get it right. When answering the question, lots of economists took "accelerating" to refer to the price level rather than inflation. I shall return to this later on.
Now, let's define what we mean by "accelerate". To do this, we can take inflation itself as an example. Suppose that last year, the general price level increased by 2%. The annual inflation rate is thus 2%. Now suppose that this year, the general price level increases by 3%. Prices have increased by 3% and inflation has increased by one percentage point. The rate at which prices are increasing has therefore itself increased. We call this increase "acceleration." It's the second derivative of price with respect to time and is expressed mathematically as d2P/dt2.
When the rate at which prices are increasing itself increases, inflation is increasing. But it is not accelerating. To make this clear, let's extend the example above by another year. Suppose, in the third year, inflation rises to 4%. The rate at which prices are increasing is clearly accelerating - in fact it has doubled in three years, which might be a matter for some concern. But the rate at which inflation is increasing has, as someone has kindly pointed out in the comments, actually fallen.
And this is where the economists went wrong. Lots of them thought "accelerating inflation" meant accelerating increase of the price level, and therefore said the answer was the second derivative of price with respect to time. But since inflation is the first derivative of price, the correct answer is actually the third derivative of price with respect to time - the change in the rate of acceleration. We express this mathematically as d3P/dt3. Physicists call it "jerk".
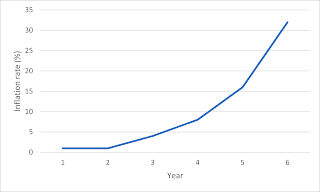
How would the numbers look if inflation really was accelerating? Let's suppose that in the fourth year, price rises really take off. Instead of prices increasing by 4%, they increase by 8%. Inflation has risen by 4%, whereas the previous year it only rose by 1%. So the rate at which inflation is increasing is accelerating. Let's imagine acceleration continues for another three years: inflation rises to 16% in year 1, 32% in year 2 and 64% in year 3 (yes, the numbers get very big very quickly when third-order acceleration takes off). If we chart the change in inflation over the course of all our examples, it looks like this:
So for economists, understanding which derivative of price is in the driving seat really, really matters. Accelerating inflation rapidly destroys an economy. Increasing inflation does not. The policy responses to accelerating and increasing inflation are likely to be quite different.
And therefore Gabriel's criticism is justified. Economists should not use "accelerate" to mean "increase". Get it right, please, economists. Your countries depend on it.
Related reading:
Covid confusion: going viral - The Mint
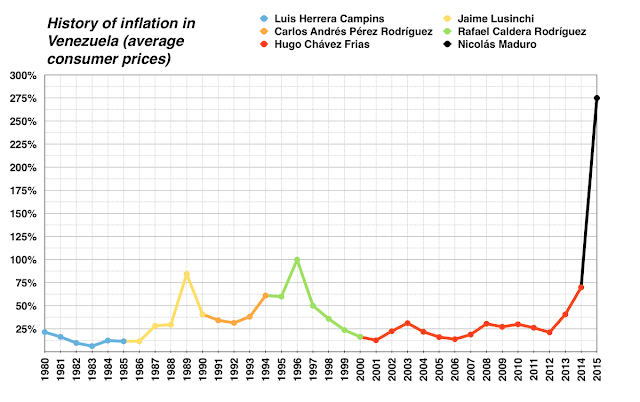
Venezuela inflation chart from Wikimedia Commons.
Racing cars picture courtesy of the U.S. Navy via Wikipedia.
